Research: Automata

Finite automata play a central role in computer science and mathematics. They are used as

acceptors, to define words and languages, and
transformers, to transform words and languages.

For finite words, both aspects of automata have been extensively studied. For infinite words (streams), the focus has been on defining streams and languages of streams; here key notions are that of

automatic sequences playing an important role in number theory, and
omega automata (e.g. Büchi, Muller, Rabin and parity automata) which form the basis of model checking and formal verification as they allow for describing the (un)acceptable behaviors of non-terminating systems such as operating systems, control systems or hardware.

Surprisingly, finite automata for transforming streams have hardly been studied. The exception are Turing machines, for which the ensuing hierarchy of stream degrees is well-known as Turing degrees. The Turing degrees are usually described as a hierarchy of degrees of sets of natural numbers (or functions over natural numbers). They can equivalently be described as a hierarchy of stream degrees since a set of natural numbers correspond to a stream (via its characteristic function). In this view, the Turing degrees arise by Turing machines transforming streams into streams. Beyond Turing machines, there has been almost no research on the power of finite automata for transforming streams.

Goal

We are interested in understanding the power of automata for transforming streams, such as finite state transducers and Mealy machines.

For the sake of this exposition, we will focus on finite state transducers. An example finite state transducer is shown in the following picture:

finite state transducer

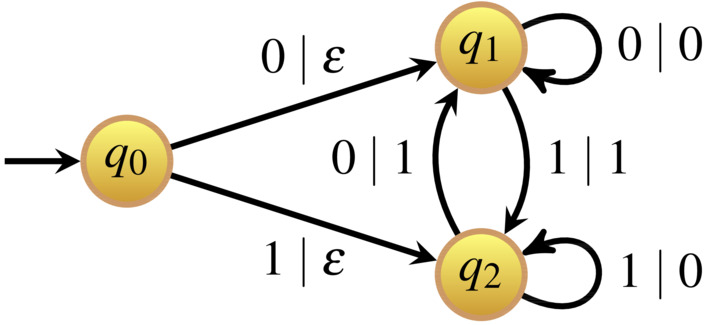
A label \( a \mid w \) along an edge indicates that the input letter is \( a \) and the output word is \( w \). The transducer reads the input stream letter by letter, in each step producing a piece of the output and changing its state. So the total output word is the concatenation of all the output words encountered along the edges.

For instance, the transducer displayed above transforms the Thue-Morse sequence \( M \) (top) the period doubling sequence \( P \) (bottom): \[ \begin{align} & 0 \;\;\; 1 \;\;\; 1 \;\;\; 0 \;\;\; 1 \;\;\; 0 \;\;\; 0 \;\;\; 1 \;\;\ldots \\ \to & \,\;\; 1 \;\;\; 0 \;\;\; 1 \;\;\; 1 \;\;\; 1 \;\;\; 0 \;\;\; 1 \;\;\ldots \end{align} \]

Background info: the period doubling sequence

The period doubling sequence \[ P = 1011 \;1010 \;1011 \;1011 \;1011\cdots \] is the solution of \[ X = 101? \;101? \;101? \;101? \;101?\cdots \] where the subsequence at the positions indicated by question marks is \( X \) itself. The period doubling sequence can also be obtained from the famous Thue-Morse sequence \[ M = 0110 1001 1001 0110 \cdots \] as the stream of differences of consecutive bits.

Mealy machines are a restricted form of finite state transducers where the output words along the edges always have length 1. So a Mealy machine outputs precisely one letter in each step, that is, for each input letter. For a finite state transducer, the output words along the edges can have arbitrary length, in particular, they can be empty.

A Simple Question without Answer

Although finite state transducers are very elegant, simple devices, we hardly understand them. There is a lack of theory about stream transducers. Even for simple examples of streams, there exist no techniques to determine whether one stream can be transformed into the other by a finite automaton. This is illustrated by the following example.

Open Problem

Take the period doubling sequence \( P \) and drop every third element: \[ \begin{align} P &= 1011 \;1010 \;1011 \;1011 \;1011 \cdots \\ Q &= 10\hphantom{1}1 \;1\hphantom{0}10 \;\hphantom{1}01\hphantom{1} \;10\hphantom{1}1 \;1\hphantom{0}11\cdots \end{align} \] It is easy to find a finite state transducer that transforms \( P \) into \( Q \). Is the reverse also possible?

Surprisingly, automata theory offers no techniques to answer such simple questions.

Degrees of Streams

We are interested in understanding transformations that finite state transducers can realize on streams. That is, we are concerned with the following transducibility relation ≥ on streams:

For streams \( s, t \) we define \( s \ge t \) if there exists a finite state transducer that transforms \( s \) into \( t \).

The transducibility relation \( \ge \) is a preorder on the set of streams. It induces equivalence classes of streams with respect to \( \ge \cap \le \), and a partial order \( > \) on these equivalence classes. We call the equivalence classes degrees, and refer to the partial order as a Transducer degrees.

So the Transducer degrees are a hierarchy of stream degrees entirely analogous to the well-known Turing degrees. The only difference is the device realizing the stream transformation.

Transducibility as a complexity measure

The transducibility relation \( \ge \) can be understood as a complexity measure. If \( s \ge t \) then the stream \( s \) is at least as complex as the stream \( t \). Streams \( s, t \) reside in the same degree if they have the same complexity, that is, \( s \) can be transformed into \( t \), and \( t \) can be transformed into \( s \).

Transducer degrees vs. Turing degrees

As finite state transducers are weaker than Turing machines, the ensuing hierarchy of Transducer degrees is much more fine-grained than the Turing degrees (the recursion-theoretic hierarchy) where all computable streams are identified in the trivial bottom degree.

As mentioned before, we hardly understand the power of finite state transducers for transforming streams. So there is a plethora of open questions about the hierarchy of Transducer degrees. The following figure depicts some initial results [1] [2] [3] [4] and open questions about this hierarchy:

hierarchy of stream degrees

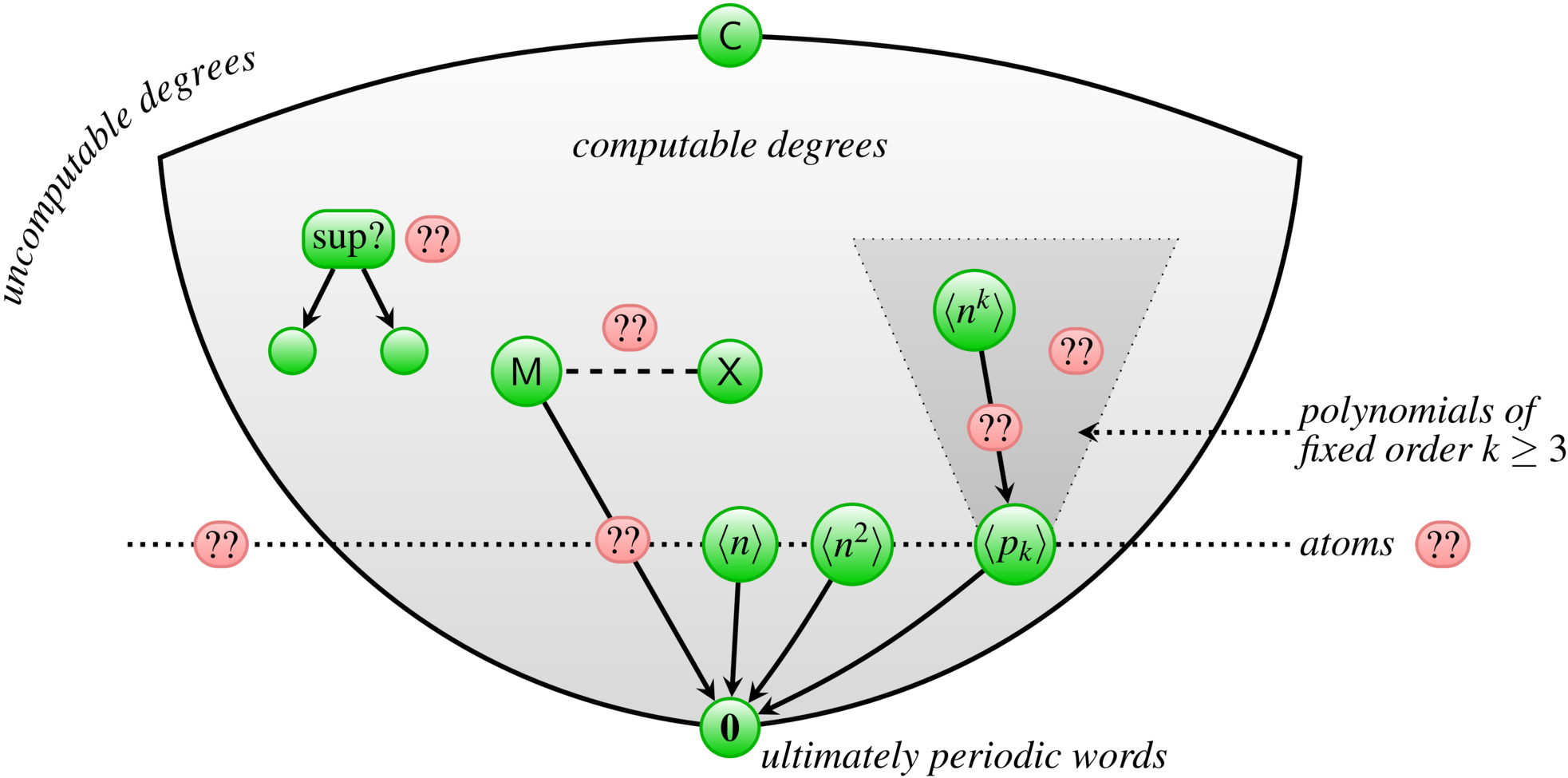
Some open problems are indicated in red. The green nodes are degrees (sets of streams). The arrows \( \to \) between degrees represent the partial order on the Transducer degrees. So an arrow \( A \to B \) means that the degree \( A \) is above \( B \) in the hierarchy. Thus every stream in \( A \) can be transformed to every stream in \( B \) by a finite state transducer, but the reverse transformation is not possible by a finite state transducer.

Notation in the figure

In the figure appear the following streams:

\( \mathbf{0} \) is the bottom degree of the hierarchy (see below),
\( M \) is the Thue-Morse sequence (see above),
\( X \) is obtained from the period doubling sequence (see above),
\( C \) is the top degree of the computable streams.

Moreover, we use the following notation: for \( f : \mathbb{N} \to \mathbb{N} \) we define the stream \[ \langle f \rangle = \prod_{i = 0}^{\infty} 0^{f(i)}1 = 0^{f(0)} \, 1 0^{f(1)} \, 1 0^{f(2)} \, \cdots\, \] and we write \( \langle f(n) \rangle \) to denote the sequence \( \langle n \mapsto f(n) \rangle \). For instance: \[ \begin{aligned} \langle n \rangle &= 1\;10\;100\;1000\;10000\;\cdots \\ \langle n^2 \rangle &= 1\;10\;10000\;1000000000\;\cdots \end{aligned} \]

Bottom degree

The bottom degree \( \mathbf{0} \) is a degree that is less or equal to all other degrees:

bottom degree

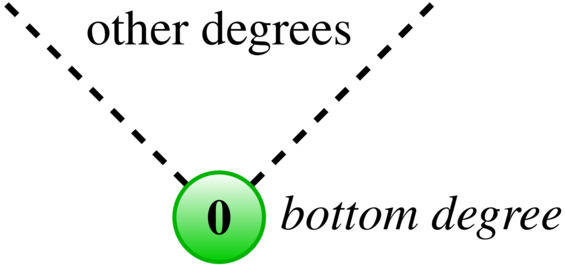
For the Transducer degrees, it consists of all ultimately periodic streams, streams of the form \( uvvvv\cdots \) for finite words \( u,v \). (For the Turing degrees the bottom degree consists of all computable streams.)

Atom degrees

An interesting concept is that of an atom degree, that is, a degree that is directly above the bottom degree with nothing in-between:

atom degree

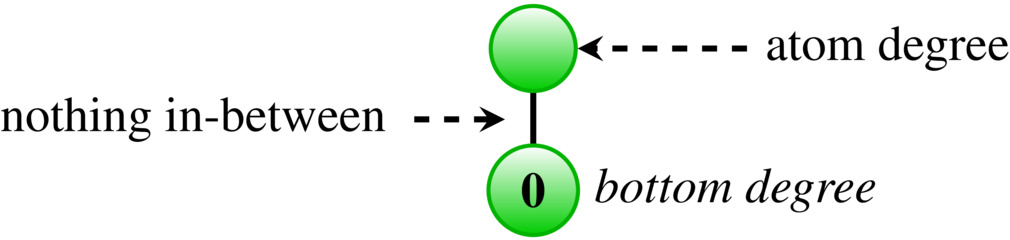
Thus the atom degrees reduce only to \( \mathbf{0} \) or themselves.

Atoms in the Turing degrees

In the Turing degrees, atoms are usually referred to as minimal degrees. A famous result about Turing degrees, obtained by Spector in 1956, is the existence of an atom degree strictly below the first Turing jump (the degree of the halting problem). In 1971, Lacombe has extended the construction of Spector to show that there are continuum many atoms in the Turing degrees.

Open questions

To mention a few open questions (there are many more):

Open Problem

Is the degree of Thue-Morse an atom?

Open Problem

Does there exist a non-computable atom in the Transducer degrees?

Open Problem

Are there continuum many atoms in the Transducer degrees?

Open Problem

Are the degrees of Thue-Morse \( M \) and Mephisto Waltz \( W \) incomparable? Here \( W \) is the morphic stream obtained as the limit of iterating the morphism \( 0\mapsto 001 \), \( 1\mapsto 110 \) on the starting word \( 0 \).

Open Problem

Does every degree have a minimal cover, that is, a degree directly above with nothing in-between?

Open Problem

When does a pair of degrees have a least upper (greatest lower) bound?

Open Problem

Are there infinite ascending (descending) sequences having a least upper (greatest lower) bound?

Open Problem

Are there interesting dense substructures?

Open Problem

Can every finite partial order be embedded in the hierarchy? Can every finite distributive lattice be embedded in the hierarchy?

Open Problem

How complex is the first-order theory in the language \( ( \ge, = ) \) ?

Open Problem

How many degrees exist among polynomials of order \( k \)? What is the structure of the degrees of polynomials?

Open Problem

Is every degree the greatest lower bound of a pair of (other) degrees?

Open Problem

Is there a degree that has precisely two degrees below itself? Is there a degree that has precisely three degrees below itself: two incomparable degrees and the bottom degree?

Relevant papers

In [1] we perform an initial investigation of the hierarchy of Transducer degrees. We show that the hierarchy is not dense and not well-founded (there are infinite descending and infinite ascending sequences). The main result in this paper is

The degree of the stream \( \langle n \rangle \) is an atom: \[ \langle n \rangle = 1\;10\;100\;1000\;10000\;100000\;\cdots \] See `Notation in the figure’ (above) for an explanation of the notation \( \langle f \rangle \).

In [2] we show that also

The degree of the stream \( \langle n^2 \rangle \) is an atom: \[ \langle n^2 \rangle = 1\;10\;10000\;1000000000\;\cdots \]

This suggests that all degrees of \( \langle n \rangle, \langle n^2 \rangle, \langle n^3 \rangle, \langle n^4\rangle,\ldots \) are atoms. Surprisingly, this is not the case, as we show in [4].

In [4] we show that techniques from continuous mathematics can be used to reason about finite state transducers. To be precise, we use the following methods from linear algebra and analysis:

continuity,
Vandermonde matrices,
invertibility of matrices, and
the generalized mean inequality.

To our best knowledge, we are the first to apply these techniques to finite state transducers – note that finite state transducers as well as streams are discrete objects. We employ these techniques to obtain both positive and negative results on transducibility. We have used (1)–(3) to establish that there exist transducers that realize certain transformations on streams. This allowed us to conclude that there is an infinite number of atoms (non-trivial, minimal degrees) in the Transducer degrees. We have employed (4) to reason about limitations of finite state transducers, to show that certain transductions are impossible. For instance, we have shown that the stream \( \langle n^3 + n^2 + n \rangle \) cannot be transformed into \( \langle n^3 \rangle \).

The main results of [4] are:

For \( k \ge 3 \), the degree of \( \langle n^k \rangle \) is not an atom.

For every \( k \ge 1 \), there is a polynomial \( p_k \) of order \( k \) such that the degree of \( \langle p_k \rangle \) is an atom. Here \[ p_k(n) = \sum_{i = 0}^{k - 1} a_i (k n + i)^k \] for some \( a_0,\ldots,a_{k-1} > 0 \). The degree \( \langle p_k \rangle \) is the unique atom among and the infimum of all the degrees of polynomials of order \( k \).

Thus there is an infinite number of atoms in the Transducer degrees. It remains open whether there are continuum many atoms.

The survey paper [3] compares the hierarchies of stream degrees arising from stream transduction as realized by

Turing machines (Turing degrees),
finite state transducers (Transducer degrees), and
Mealy machines (Mealy degrees).

We compare central properties of these hierarchies. We summarize our main results on Transducer degrees and also related results on Turing degrees and Mealy degrees.

In [5] we show that non-erasing transductions (no empty words along the edges) preserve a condition called alpha-substitutivity. Roughly, a sequence is alpha-substitutive if the sequence can be obtained as the limit of iterating a substitution with dominant eigenvalue alpha. This result can be applied to prove that certain transformations are not possible using non-erasing transducers. Unfortunately, this result does not not generalise to general finite state transducers (which can have empty words along the edges), and therefore cannot be applied to reason about the Transducer degrees.

In [6] we consider finite automata (not finte state transducers). Most properties of finite automata are decidable. In [6] we give some examples of undecidable properties.

Research: Automata

A Simple Question without Answer

Degrees of Streams

Bottom degree

Atom degrees

Open questions

Relevant papers

References

Bibtex

Digital Object Identifier

Summary

Bibtex

Digital Object Identifier

Summary

Bibtex

Digital Object Identifier

Summary

Bibtex

Digital Object Identifier

Summary

Bibtex

Digital Object Identifier

Summary

Bibtex

Digital Object Identifier