Research: Confluence
Confluence is a central property of rewrite systems, and it plays an important role for:
- program correctness as it guarantees uniqueness of results (normal forms), and
- model checking where it is employed for state space reduction.
Confluence
A binary relation \( \to \) on a set \( A \) is confluent if \( \forall a,b,c \in A. \) \[ b \leftarrow^* a \to^* c \implies \exists d.\; b \to^* d \leftarrow^* c \]
In other words, \( \to \) is confluent if \( {\leftarrow^* \cdot \to^*} \subseteq {\to^* \cdot \leftarrow^*} \). This can be illustrated as follows:
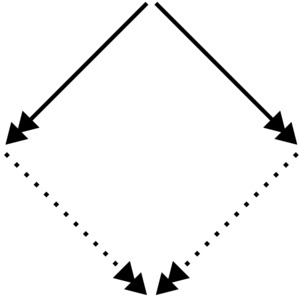
Here we write \( \twoheadrightarrow \) for \( \to^* \), the reflexive, transitive closure of \( \to \). The solid lines stand for universal quantification, and the dotted lines for existential quantification.
Decreasing Diagrams & Weak Diamond Property
The decreasing diagrams technique is one of the strongest and most versatile methods for proving confluence. It is complete for countable systems, and it has many well-known confluence criteria as corollaries, for instance:
- Newman’s lemma,
- Huet’s strong confluence.
- the lemma of Hindley–Rosen, and
- Rosen’s request lemma.
The way to decreasing diagrams was paved by De Bruijn in 1978 in a note describing the weak diamond property, with a proof based on an intricate induction. The search for an elegant proof led van Oostrom in 1994 to the decreasing diagrams technique.
The weak diamond property and decreasing diagrams have many similarities. The basic idea of both techniques is to employ a labeling of the steps in order to conclude confluence from local confluence. Local confluence (\( {\leftarrow \cdot \to} \subseteq {\to^* \cdot \leftarrow^*} \)) itself is not sufficient for confluence. To this end, both methods exploit the labeling of the steps to impose additional requirements on the joining reductions, as displayed in the following figure:
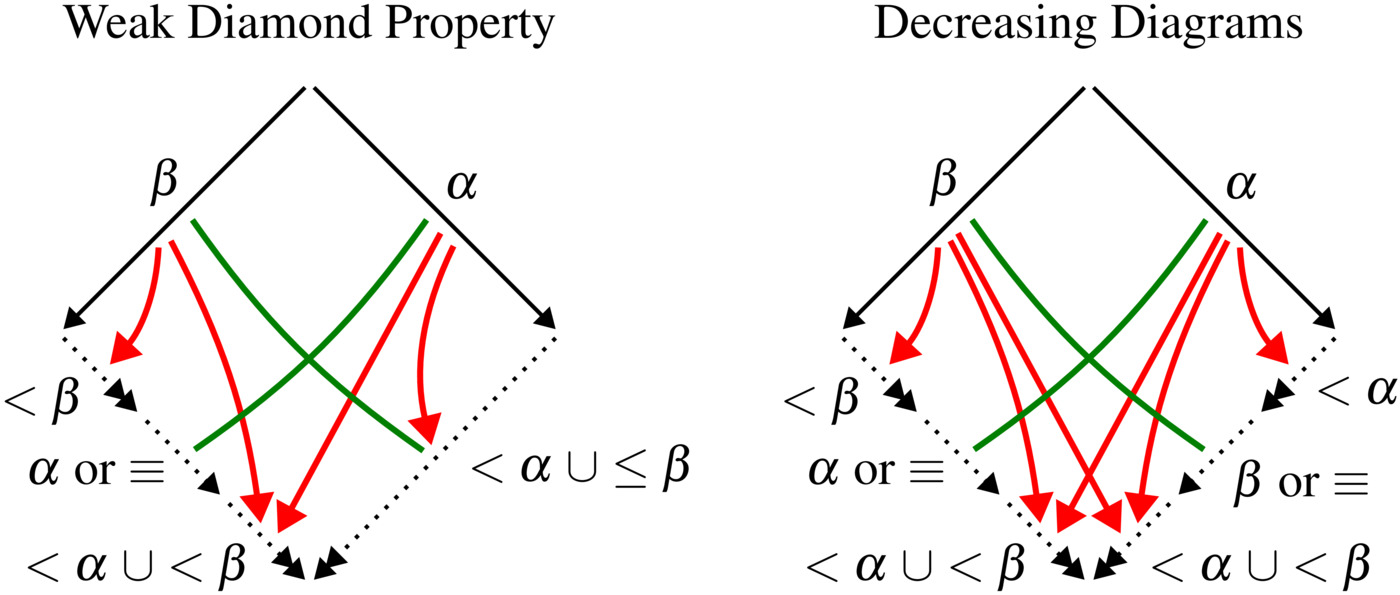
The red and green lines inside the diagrams are just a visual aid. The red lines indicate a strict decrease of the label, the green lines a weak decrease.
Weak Diamond Property - De Bruijn (1978)
A relation \( \to \) is confluent if the steps can be labeled with labels from a well-founded total order \( < \) such that every peak \[ c \stackrel{\beta}{\leftarrow} a \stackrel{\alpha}{\to} b \] with \( \boldsymbol{\beta \le \alpha} \) can be joined by reductions of the form of the weak diamond property (above).
Decreasing Diagrams - Van Oostrom (1994)
A relation \( \to \) is confluent if the steps can be labeled with labels from a well-founded partial order \( < \) such that every peak \[ c \stackrel{\beta}{\leftarrow} a \stackrel{\alpha}{\to} b \] can be joined by reductions of the form of the decreasing diagram (above).
So the differences between the weak diamond property and decreasing diagrams concern the use of total vs. partial orders, and the symmetry in the decreasing diagram.
Our contribution
De Bruijn’s note on the weak diamond property is a seminal work as it pioneers the key ingredients (the labeling and the shape of the diagrams) that make decreasing diagrams so strong. Nevertheless, the weak diamond property has almost been forgotten over time.
In [1], we show that the weak diamond property and decreasing diagrams have equal strengths. Given a confluence proof using decreasing diagrams, we obtain a proof using the weak diamond property by transforming the partial order on the labels into a total order. We demonstrate that this does not require the Axiom of Choice as we can identify elements of equal `ordinal height’. Previously, it has been known that the decreasing diagrams technique subsumes the weak diamond property, but the reverse has not been known.
In [1], we moreover give a new proof of confluence by decreasing diagrams. Our proof is just about one page long, and is one of the shortest proofs of confluence by decreasing diagrams.
Finally, we prove in [1] that decreasing diagrams are not complete for proving commutation of countable (even finite) systems (while they are complete for confluence of countable systems).
In [2], we investigate how the size of the label set influences the strength of decreasing diagrams. Surprisingly, we find that two labels suffice for proving confluence of every countable confluent system. This stands in sharp contrast to the situation for commutation, where two labels do not suffice. We construct, for every \( n \in \mathbb{N} \), a rewrite system that can be proven commutating using \( n \) labels but not with less labels.
Open problems
Considering the importance and wide use of decreasing diagrams, it is surprising that it has remained open since 1993 whether decreasing diagrams are complete for uncountable systems:
Open Problem (#56 on the RTA List of Open Problems)
Is decreasing diagrams complete for proving confluence of uncountable systems?
Our results in [2] suggest that it may be fruitful to first answer the following question:
Open Problem
Is there a uncountable confluent system that cannot be proven confluent by decreasing diagrams with two labels?
References
- De Bruijn’s Weak Diamond Property RevisitedJörg Endrullis, and Jan Willem KlopIndagationes Mathematicae , 24 (4) , pp. 1050–1072 (2013)
- Decreasing Diagrams with Two Labels Are Complete for Confluence of Countable SystemsJörg Endrullis, Jan Willem Klop, and Roy OverbeekIn: Proc. Conf. on Formal Structures for Computation and Deduction (FSCD 2018), pp. 14:1–14:15, Schloss Dagstuhl - Leibniz-Zentrum fuer Informatik (2018)