\begin{frame}
  \small
  
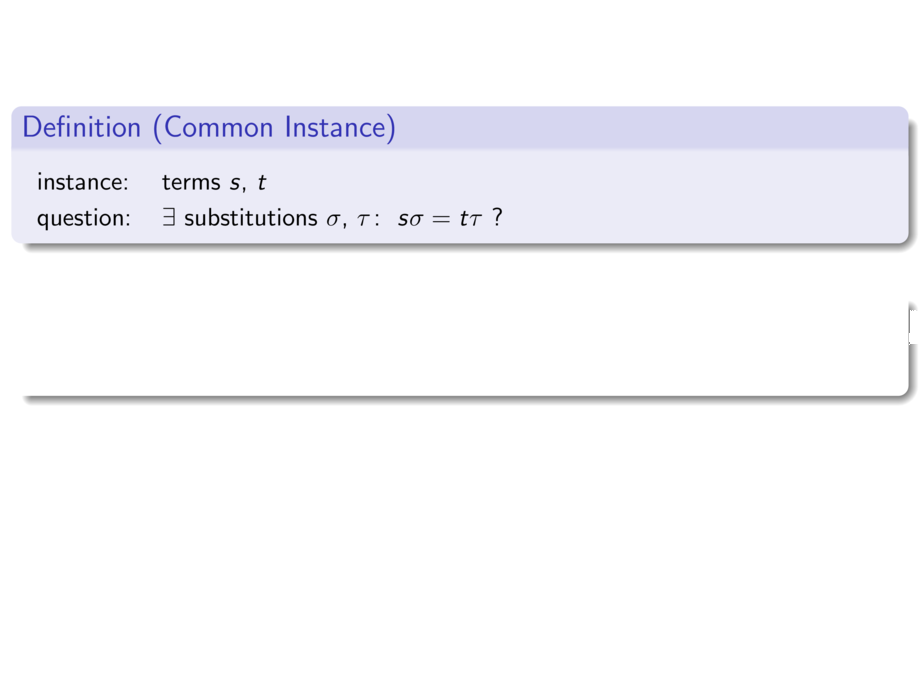
  \begin{definition}[Common Instance]
  \smallskip
  \begin{tabular}{ll@{\qquad\qquad}ll}
  instance: & terms $s$, $t$ \\[.5ex]
  question: & $\exists$
  $\mathstrut\text{substitutions $\sigma$, $\tau$}\colon ~ s\sigma = t\tau$ ?
  \end{tabular}
  \end{definition}
  \pause\medskip

  \begin{definition}
    \alert{most general} common instance (\alert{mgci})
    is at least as general as any other common instance 
  \end{definition}  
  \pause\medskip

  We can compute the most general common instance as follows:
  \begin{itemize}
  \pause
    \item let $\gamma$ be a renaming of the variables in $t$\\ such that $s$ and $t\gamma$ have no variables in common
  \pause
    \item if $\rho$ is the mgu for $s$ and $t\gamma$, then $s\rho = t\gamma\rho$ is the mgci for $s$ and $t$
%   \pause
%     \item if $\sigma$ exists, then $s\sigma = t (\gamma\sigma)$ is the mgci\\
%           (with substitutions $\sigma$ and $\gamma\sigma$, respectively)
  \end{itemize}
\end{frame}