\begin{frame}
  \small
  
  \begin{definitions}
  \begin{itemize}
  \item
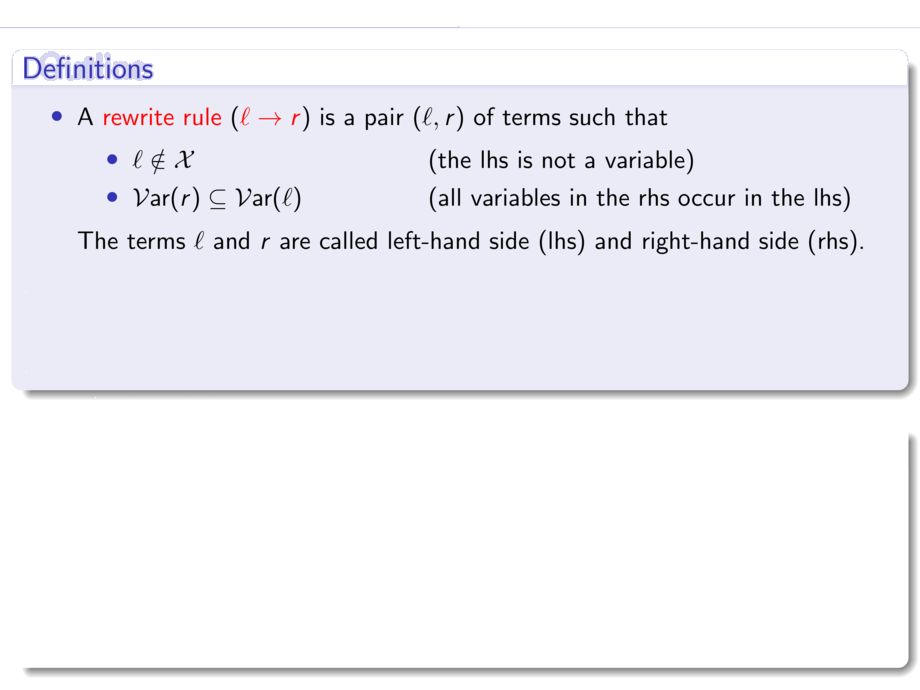
    A \alert<1>{rewrite rule} (\alert<1>{$\ell \to r$}) is a pair $(\ell,r)$ of terms such that
    \begin{itemize}
    \item
    \makebox[4cm][l]{$\ell \notin \VV$} (the lhs is not a variable)
    \smallskip
    \item
    \makebox[4cm][l]{$\Var(r) \subseteq \Var(\ell)$} (all variables in the rhs occur in the lhs)
    \end{itemize}
    The terms $\ell$ and $r$ are called left-hand side (lhs) and right-hand side (rhs).
  \item<2->
  A \alert<2>{term rewrite system} (\alert<2>{TRS}) is pair $\TRS$ consisting
  of
  \begin{itemize}
  \item
  \makebox[1cm][l]{$\FF$} signature
  \smallskip
  \item
  \makebox[1cm][l]{$\RR$} set of rewrite rules between terms in
  $\TT(\FF,\VV)$
  \end{itemize}
  \end{itemize}
  \end{definitions}
  
  \begin{example}<3->
  \smallskip
  TRS $\TRS$ with signature $\FF$
  \vspace{-1.5ex}
  \[
  \mG{0} ~ (\text{constant}) \qquad
  \mG{s} ~ (\text{unary}) \qquad
  \mG{add} ~ (\text{binary})
  \]\\[-1.5ex]
  $\arity{\m{0}} = 0$, $\arity{\m{s}} = 1$, $\arity{\m{add}} = 2$, and rewrite rules $\RR$
  \vspace{-1.5ex}
  \[
  \GREEN{\begin{array}{r@{~}c@{~}l}
  \m{add}(\m{0},y) & \to & y \\[.5ex]
  \m{add}(\m{s}(x),y) & \to & \m{s}(\m{add}(x,y)) 
  \end{array}}
  \]
  \end{example}

\end{frame}