




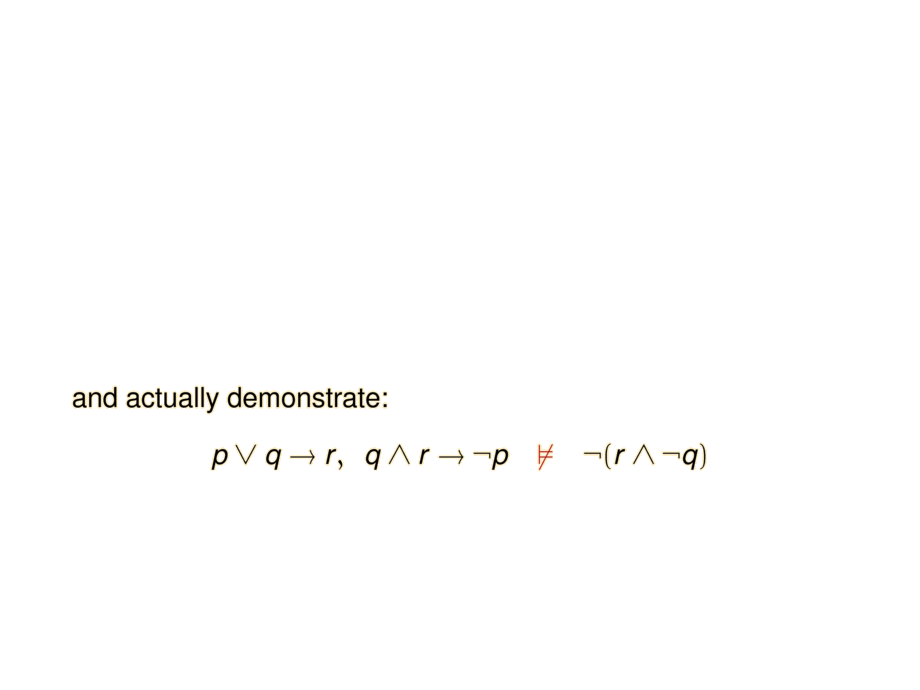






























































































7/270
\begin{frame}
\frametitle{Usefulness of Semantics}
Can we prove the following by natural deduction?
\begin{center}
$
\formula{\logimp{\logor{\prop{p}}{\prop{q}}}{\prop{r}}}, \;\;
\formula{\logimp{\logand{\prop{q}}{\prop{r}}}{\lognot{\prop{p}}}}
\;\;\derives\;\;
\formula{\lognot{(\logand{\prop{r}}{\lognot{\prop{q}})}}}
$
\end{center}\pause{}
What if it is not derivable? \pause \alert{Might be difficult to show.}
\pause\smallskip
\begin{goal}{}
Using the \emph{soundness and completeness theorem}
we could concentrate on the \emph{equivalent semantic entailment}:
\begin{center}
$
\formula{\logimp{\logor{\prop{p}}{\prop{q}}}{\prop{r}}}, \;\;
\formula{\logimp{\logand{\prop{q}}{\prop{r}}}{\lognot{\prop{p}}}}
\;\;\satisfies\;\;
\formula{\lognot{(\logand{\prop{r}}{\lognot{\prop{q}})}}}
$
\end{center}\pause{}
and actually demonstrate:
\begin{center}
$
\logimp{\logor{\prop{p}}{\prop{q}}}{\prop{r}}, \;\;
\logimp{\logand{\prop{q}}{\prop{r}}}{\lognot{\prop{p}}}
\;\;\satisfiesnot\;\;
\lognot{(\logand{\prop{r}}{\lognot{\prop{q}})}}
$
\end{center}
\end{goal}
\pause\smallskip
That is, find a valuation $\saval$ such that
\begin{align*}
\aval{\formula{\logimp{\logor{\prop{p}}{\prop{q}}}{\prop{r}}}} & = \True
\\
\aval{\formula{\logimp{\logand{\prop{q}}{\prop{r}}}{\lognot{\prop{p}}}}} & = \True
\\
\aval{\formula{\lognot{(\logand{\prop{r}}{\lognot{\prop{q}})}}}} & = \False
\end{align*}
\end{frame}

