\begin{frame}
  \frametitle{Finding a Tangent}
  
  \begin{block}{}
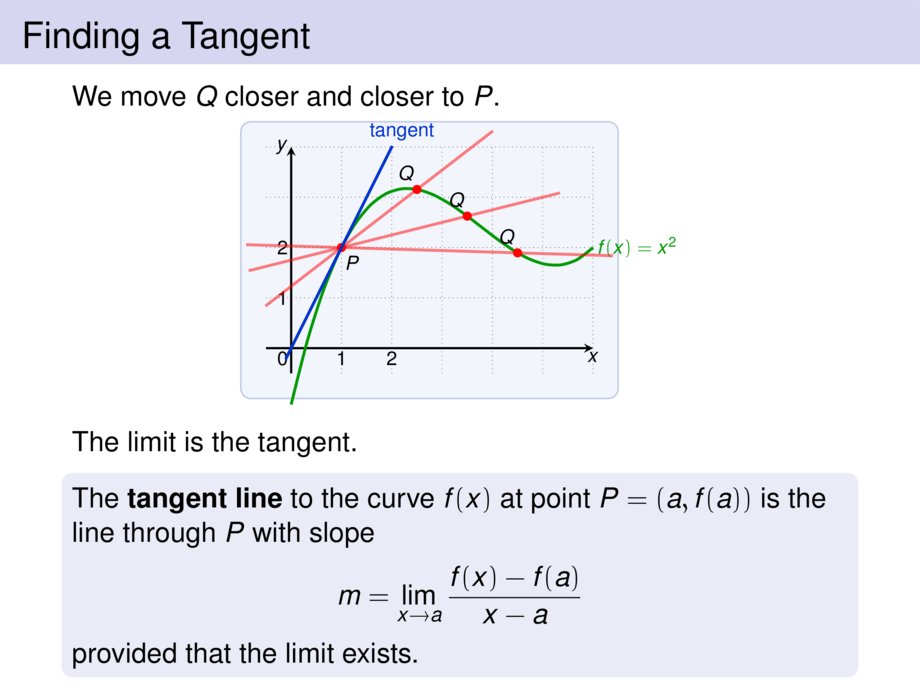
    The \emph{tangent line} to the curve $f(x)$ at point $P = (a,f(a))$
    is the line through $P$ with slope
    \begin{talign}
      m = \lim_{x\to a} \frac{f(x) - f(a)}{x - a}
    \end{talign}
    provided that the limit exists.
  \end{block}
  \pause\medskip
  
  \begin{exampleblock}{}
    Find an equation of the tangent line to $f(x) = x^2$ at point $(1,1)$.
    \pause\medskip
    
    We use the equation for the slope with $a = 1$:
    \begin{talign}
      m 
      &= \lim_{x\to a} \frac{f(x) - f(a)}{x - a}
      \mpause[1]{= \lim_{x\to 1} \frac{f(x) - f(1)}{x - 1}}
      \mpause[2]{= \lim_{x\to 1} \frac{x^2 - 1}{x - 1}}\\
      &\mpause[3]{= \lim_{x\to 1} \frac{(x + 1)(x-1)}{x - 1}}
       \mpause[4]{= \lim_{x\to 1} (x + 1)}
       \mpause[5]{= 2}
    \end{talign}
    \pause[9]
    Thus $y - 1 = 2 (x-1)$\pause, that is, the tangent is $y = 2x - 1$. 
  \end{exampleblock}
  \vspace{10cm}
\end{frame}