\begin{frame}
  \frametitle{Finding a Tangent}
  
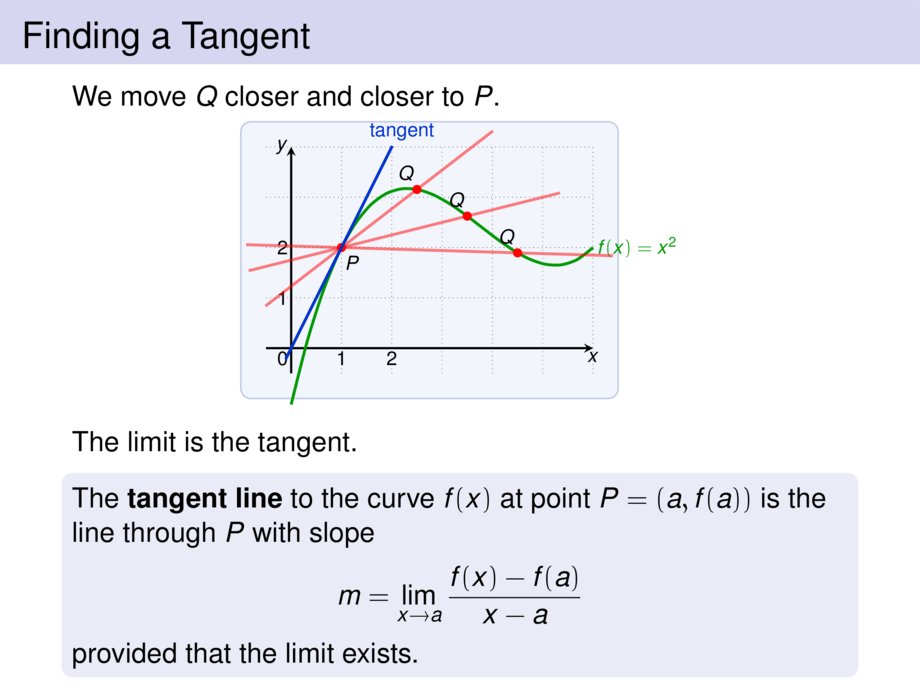
  We move $Q$ closer and closer to $P$.
  \begin{center}
  \scalebox{.7}{
  \begin{tikzpicture}[default]
    \diagram{-.5}{6}{-.5}{4}{1}
    \diagramannotate

    \draw[name path=x2,ultra thick,cgreen] plot[smooth,domain=-0:6,samples=20] function{3-(x-2)**2 + 0.12*(x-1)**3} node[right] {$f(x) =x^2$};

    \node[dot] (P) at (1,{2}) {};
    \node[anchor=north west,at=(P.south)] {$P$};

    \foreach \x in {4.5,3.5,2.5} {
      \node[dot] (Q) at (\x,{3-pow(\x-2,2) + 0.12*pow(\x-1,3)}) {};
      \node[anchor=south east,at=(Q.north)] {$Q$};
      \through[opacity=.5,red,ultra thick]{2cm}{2cm}{P}{Q}
    }

    \tangent[cblue,ultra thick]{55}{50}{3-pow(\x-2,2) + 0.12*pow(\x-1,3)}{1}
    \node[cblue] at (2.2,4.3) {tangent};
  \end{tikzpicture}
  }
  \end{center}
  \pause
  The limit is the tangent.
  \pause

  \begin{block}{}
    The \emph{tangent line} to the curve $f(x)$ at point $P = (a,f(a))$
    is the line through $P$ with slope
    \begin{talign}
      m = \lim_{x\to a} \frac{f(x) - f(a)}{x - a}
    \end{talign}
    provided that the limit exists.
  \end{block}
\end{frame}