\begin{frame}
  \frametitle{Limit: Caution with Calculators}

  \begin{exampleblock}{}
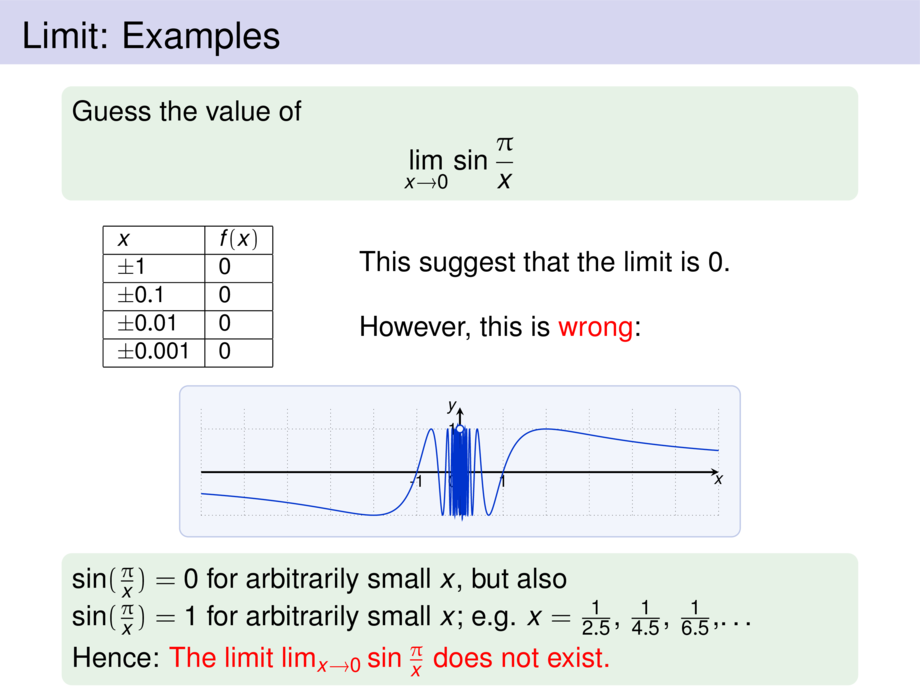
    Guess the value of
    \begin{talign}
      \lim_{x\to 0} \frac{\sqrt{x^2 + 9} -3}{x^2}
    \end{talign}
  \end{exampleblock}
  
  \onslide<6->{
  \begin{center}
    \scalebox{.7}{
    \begin{tikzpicture}[default,yscale=2,xscale=.5]
      {\def\diaborderx{1cm}
       \def\diabordery{.3cm}
      \diagram[1]{-5}{5}{0}{1.2}{1}}
      \diagramannotatex{0,1,2,3}
      \diagramannotatey{0.5,1}
      \draw[cgreen,ultra thick] plot[smooth,domain=-5:5,samples=20] function{(sqrt(x**2 + 9) -3) / (x**2)};
  
      \def\x{0}
      \def\y{{.166666666}}
      \node[exclude={cgreen}] at (\x,\y) {};
    \end{tikzpicture}
    }\quad\quad
    \scalebox{.7}{
    \begin{tikzpicture}[default,scale=5]
      {\def\diaborderx{.1cm}
       \def\diabordery{.1cm}
      \diagram[.1]{-.5}{.5}{0}{.5}{1}}
      \diagramannotatex{0,0.2,0.4}
      \diagramannotatey{0.1,0.3}
      \draw[cgreen,ultra thick] plot[smooth,domain=-.5:.5,samples=20] function{(sqrt(x**2 + 9) -3) / (x**2)};
  
      \def\x{0}
      \def\y{{.166666666}}
      \node[exclude={cgreen}] at (\x,\y) {};
    \end{tikzpicture}
    }
  \end{center}
  }
  \pause
    
  \begin{minipage}{.37\textwidth}
  {\small
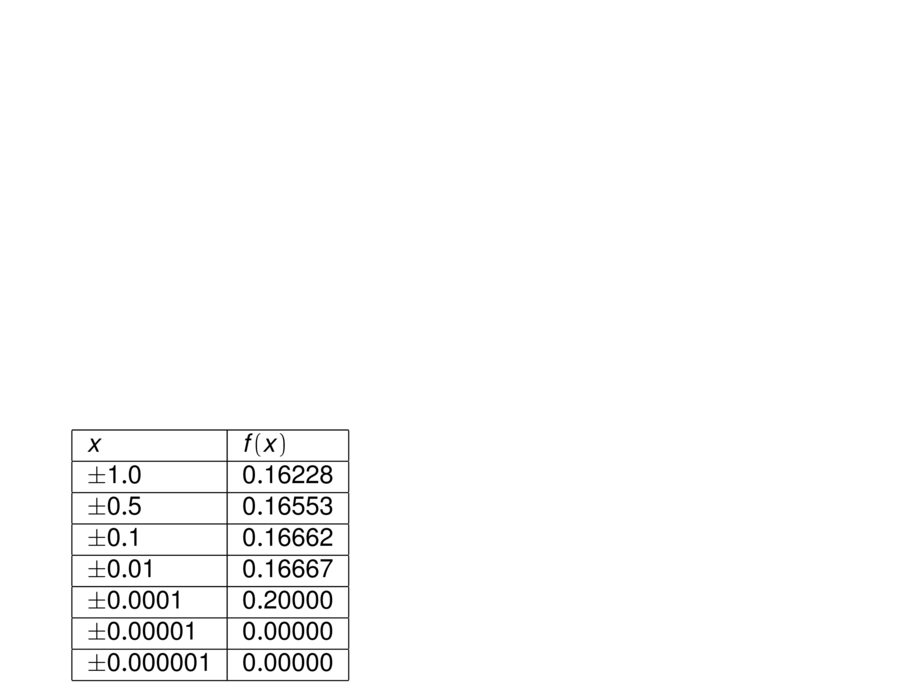
  \begin{tabular}{|l|l|}
    \hline
    $x$ & $f(x)$ \\
    \hline
    $\pm 1.0$ & $0.16228$ \\
    \hline
    $\pm 0.5$ & $0.16553$ \\
    \hline
    $\pm 0.1$ & $0.16662$ \\
    \hline
    $\pm 0.01$ & $0.16667$ \\
    \hline
    $\pm 0.0001$ & $0.20000$ \\
    \hline
    $\pm 0.00001$ & $0.00000$ \\
    \hline
    $\pm 0.000001$ & $0.00000$ \\
    \hline
  \end{tabular}
  }
  \end{minipage}~~~
  \begin{minipage}{.62\textwidth}
    \pause
    Is the limit $0$? \pause \alert{NO}
    \medskip\pause
    
    Problem: calculator gives wrong values!
%     The calculator has only a fixed number of digits, and needs to round.
    For small $x$ it rounds $\sqrt{x^2+9} - 3$ to $0$.
    \pause\medskip
    
    \begin{exampleblock}{}
      The correct limit is $\frac{1}{6} = 0.166666 \ldots$
    \end{exampleblock}
  \end{minipage}

  \vspace{10cm}
\end{frame}