

































































































12/122
\begin{frame}
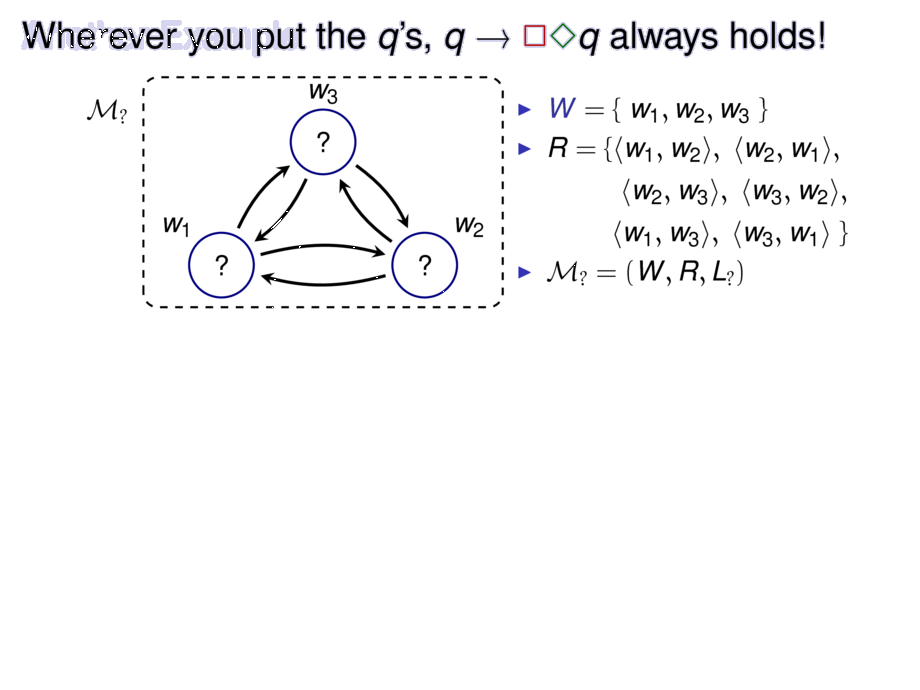
\frametitle{Wherever you put the $q$'s, $q \to \all \some q$ always holds!}
\begin{minipage}{0.53\textwidth}
\begin{center}
\begin{tikzpicture}[
default,
point/.style={circle, draw=blue, thick, inner sep=3pt, minimum size=9mm},
node distance=20mm]
\node (3) [point] {?};
\node [ao=3] {$w_3$};
\node (2) [point, below right of=3,yshift=-3mm] {?};
\node [aro=2] {$w_2$};
\node (1) [point, below left of=3,yshift=-3mm] {?};
\node [alo=1] {$w_1$};
\begin{scope}[shorten <= 1mm, shorten >= 1mm, very thick,>=stealth]
\draw [->] (1) to[bend left=15] (2);
\draw [->] (2) to[bend left=15] (1);
\draw [->] (2) to[bend left=15] (3);
\draw [->] (3) to[bend left=15] (2);
\draw [->] (3) to[bend left=15] (1);
\draw [->] (1) to[bend left=15] (3);
\end{scope}
\draw [rounded corners=2mm, dashed] (-25mm,-23mm) rectangle (25mm,9mm);
\node at (-25mm,8mm) [anchor=north east,inner sep=2mm] {$\mathcal{M}_?$};
\end{tikzpicture}
\end{center}
\end{minipage}~%
\begin{minipage}{0.46\textwidth}
\begin{itemize}
\item $\BLUE{W}= \{\;w_1,w_2,w_3\;\}$
\item $R = \{\pair{w_1}{w_2},\; \pair{w_2}{w_1},$ \\
\;\hfill $\pair{w_2}{w_3},\; \pair{w_3}{w_2}, $ \\
\;\hfill $\pair{w_1}{w_3},\; \pair{w_3}{w_1}\;\}$
\item $\M_? = (W,R,L_?)$
\end{itemize}
\end{minipage}
\smallskip\pause
\begin{exampleblock}{We check one world ($w_1$), with and without $q$}
\begin{itemize}
\pause
\item Assume that $q \not\in L_?(w_1)$, \pause \\
then $w_1 \fc q \to\all\some q$ \tabto{4.5cm} since $\;w_1 \not\fc q$
\pause
\item Assume that $q \in L_?(w_1) $, \\
\mpause[4]{then $w_1 \fc q \to \all\some q$
\tabto{4.5cm} since}\mpause[3]{ $\;w_1 \fc \all\some q$
\tabto{4.5cm} since}\mpause[2]{ $\;w_2 \fc \some q$ and $\;w_3 \fc \some q$
\tabto{4.5cm} since}\mpause[1]{ $\;w_1\fc q$ }
\end{itemize}
\end{exampleblock}
\pause\pause\pause\pause\pause
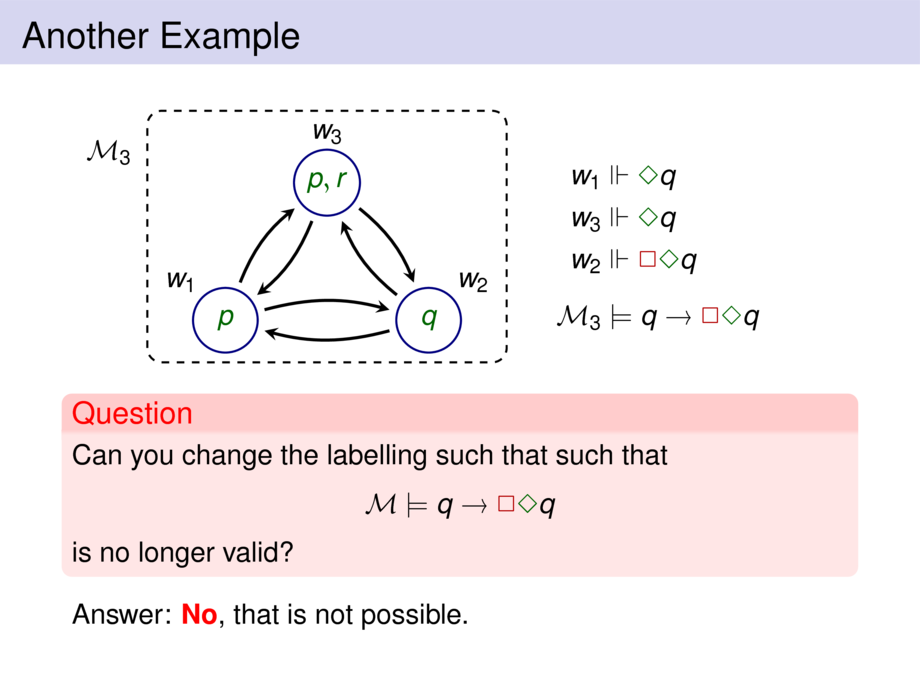
\emph{Because of the arrow configuration} (always back and forth),
$q \to \all\some q$ is \emph{always valid} wherever you put the $q$'s.
\bigskip
\end{frame}

