\begin{frame}{Bounded Tiling Problem}
  \begin{block}{}
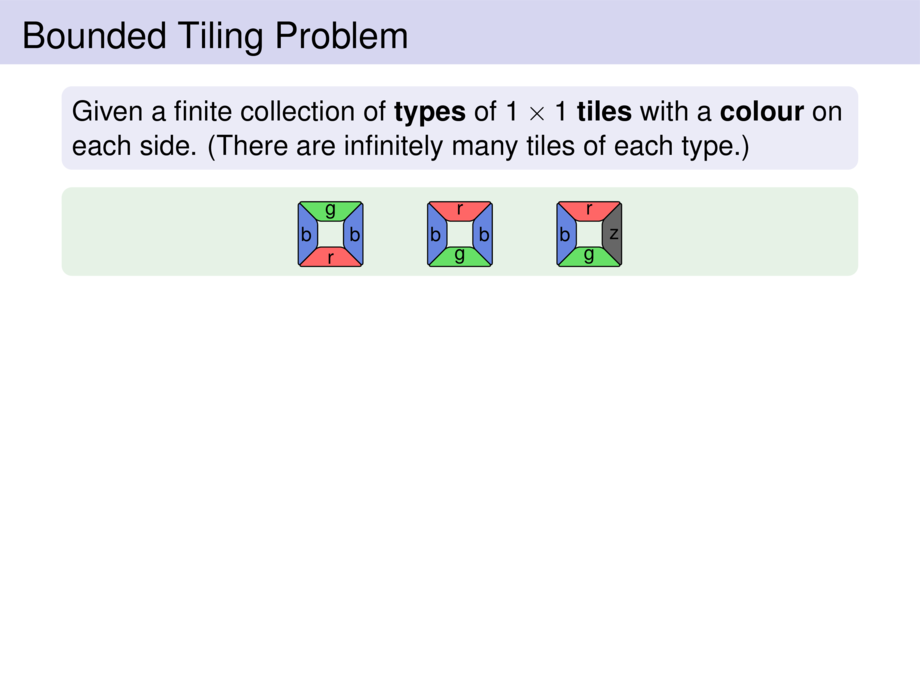
    Given a finite collection of \emph{types} of $1 \times 1$ \emph{tiles} with a \emph{colour} on each side.
    (There are infinitely many tiles of each type.) 
  \end{block}
  
  \begin{exampleblock}{}
    \begin{center}
      \begin{tikzpicture}[default,scale=.9]
        \tile{0}{0}{g}{b}{r}{b}
        \tile{2}{0}{r}{b}{g}{b}
        \tile{4}{0}{r}{z}{g}{b}
      \end{tikzpicture}
    \end{center}
  \end{exampleblock}
  \pause
  
  \begin{goal}{}
    \emph{Bonded tiling problem}: the input is
    $n \in \mathbb{N}$,
    a finite collection of types of tiles,
    the first row of $n$ tiles.
    \smallskip

    \alert{Is it possible to tile an $n \times n$ field (with the given first row)?}
    \smallskip
    
    When connecting tiles, the touching side must have the same colour.
    Tiles must not be rotated.
  \end{goal}
  \pause

  \begin{exampleblock}{}
    Example $n = 2$:\vspace{-3.5ex}
    \begin{center}
      \begin{tikzpicture}[default,scale=.9]
        \tile{0}{0}{g}{b}{r}{b}
        \tile{1}{0}{r}{b}{g}{b}
        \node [scale=.7,anchor=north,rectangle] at (1,-.1) {first row};
        \node [scale=.7,anchor=north,rectangle] at (4,-.1) {incomplete tiling};
        \node [scale=.7,anchor=north,rectangle] at (7,-.1) {correct tiling};
        
        \tile{3}{0}{g}{b}{r}{b}
        \tile{4}{0}{r}{b}{g}{b}
        \tile{3}{1}{r}{z}{g}{b}

        \tile{6}{0}{g}{b}{r}{b}
        \tile{7}{0}{r}{b}{g}{b}
        \tile{6}{1}{r}{b}{g}{b}
        \tile{7}{1}{g}{b}{r}{b}
      \end{tikzpicture}\vspace{-.5ex}
    \end{center}
  \end{exampleblock}
\end{frame}