


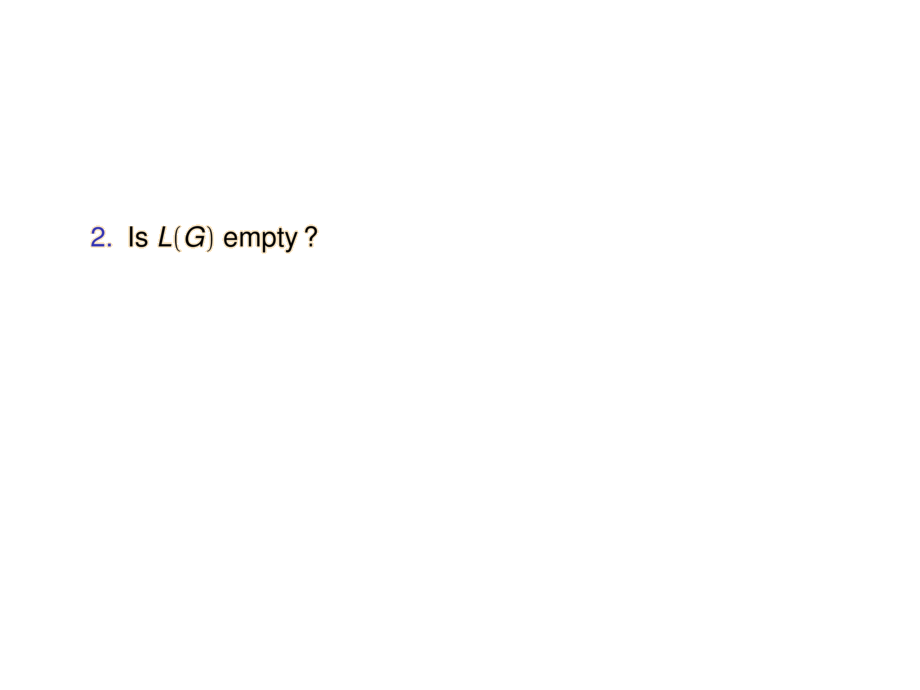
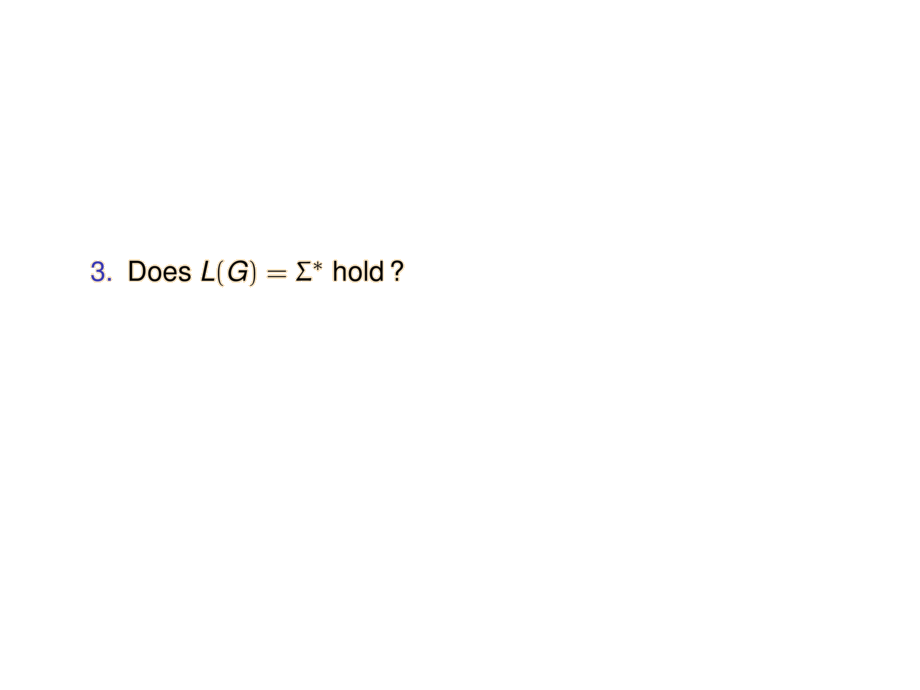
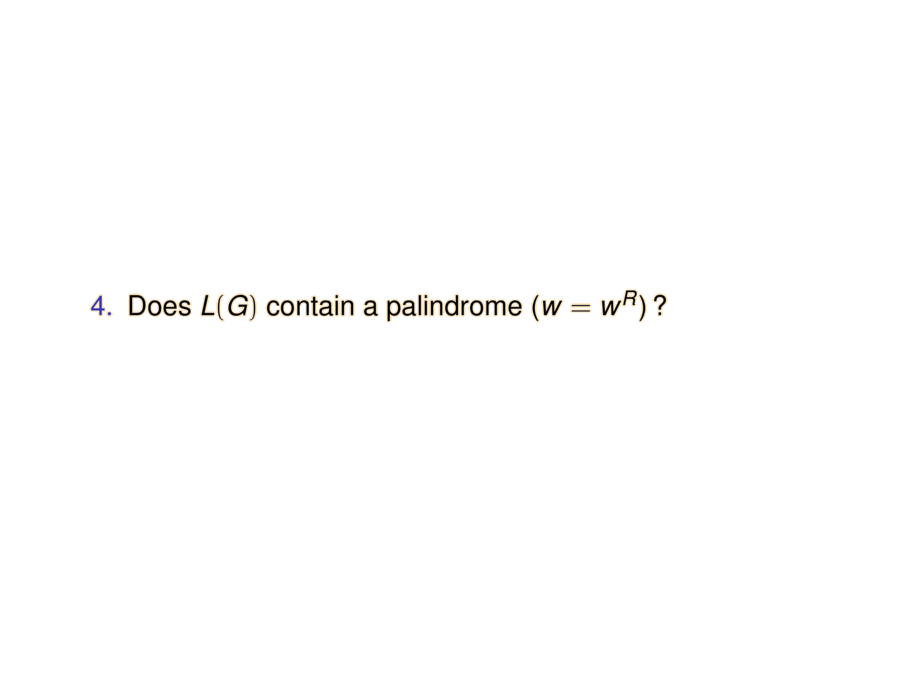
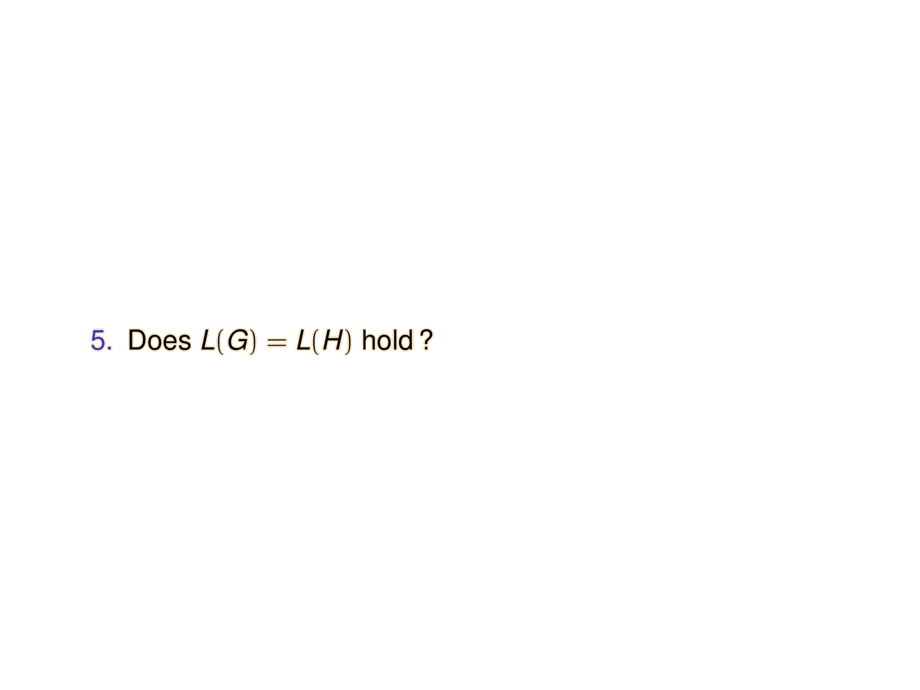
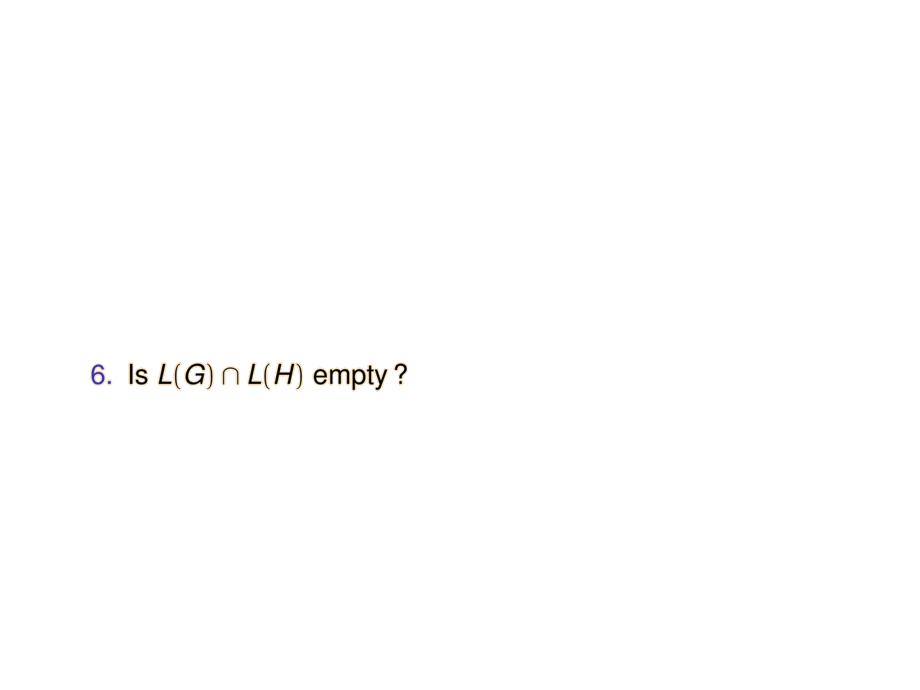




























































































43/46
\begin{frame}{Basic Questions about Context-Free Grammars}
\begin{goal}{}
Given context-free grammar $G$ and $H$.
\medskip
Which of the following questions are \emph{decidable}?
\begin{enumerate}\setlength{\itemsep}{0pt}
\pause
\item Given $w \in \Sigma^*$, do we have $w \in L(G)$\,?
\pause
\item Is $L(G)$ empty\,?
\pause
\item Does $L(G) = \Sigma^*$ hold\,?
\pause
\item Does $L(G)$ contain a palindrome ($w = w^R$)\,?\\
\pause
\item Does $L(G) = L(H)$ hold\,?
\pause
\item Is $L(G) \cap L(H)$ empty\,?
\end{enumerate}
\end{goal}
\pause
\begin{alertblock}{}
Only the first two questions are decidable.
\end{alertblock}
\pause
\begin{block}{}\setlength{\itemsep}{0pt}
Remove all $\lambda$ and unit productions.
\begin{enumerate}
\item $\{\, v \mid S \Rightarrow^* v,\; |v|\leq|w| \,\}$ can be computed in finite time.
\item $L(G)$ is empty $\iff$ starting variable is useless.
\end{enumerate}
\end{block}
\pause
\structure{Surprisingly} all other questions are undecidable.
\bigskip
\end{frame}

