



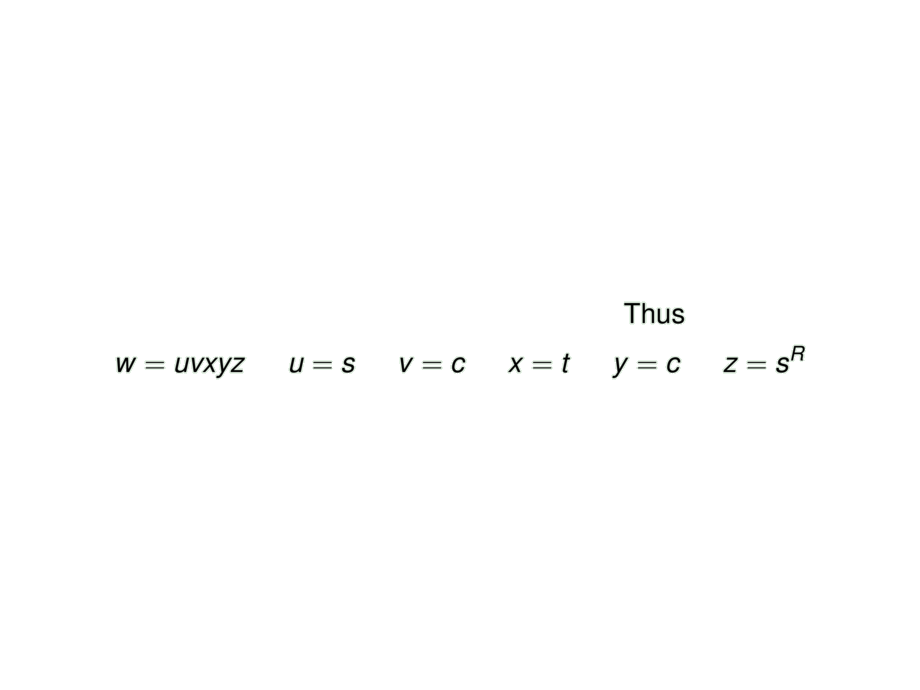































































































40/55
\begin{frame}{Exercises (2)}
\begin{exampleblock}{}
Show $L = \{\, w \in \{a,b\}^* \mid w=w^R \,\}$ for has the pumping property.
\pause\medskip
Let $m =3$. \pause Every word $w \in L$ with $|w| \ge m$ has the form
\begin{talign}
w = sctcs^R
\end{talign}
where $s \in \{a,b\}^*$, $c \in \{a,b\}$ and $t \in \{\, a,b,\lambda \,\}$.
\pause
Thus
\begin{talign}
w &= uvxyz &
u &= s &
v &= c &
x &= t &
y &= c &
z &= s^R
\end{talign}
\pause
We have $|vxy| \le m$, $|vy| \ge 1$\pause and
\begin{talign}
uv^ixy^iz = s c^{i} t c^{i} s^R \in L
\end{talign}
for every $i \ge 0$.
\pause
Thus the language has the pumping property.
\end{exampleblock}
\pause
\begin{exampleblock}{}
Show that $L$ also has the pumping property for $m = 2$.\\[1ex]
\emph{Hint:} distinguish $w$ of even and odd length when splitting.
\end{exampleblock}
\end{frame}

