


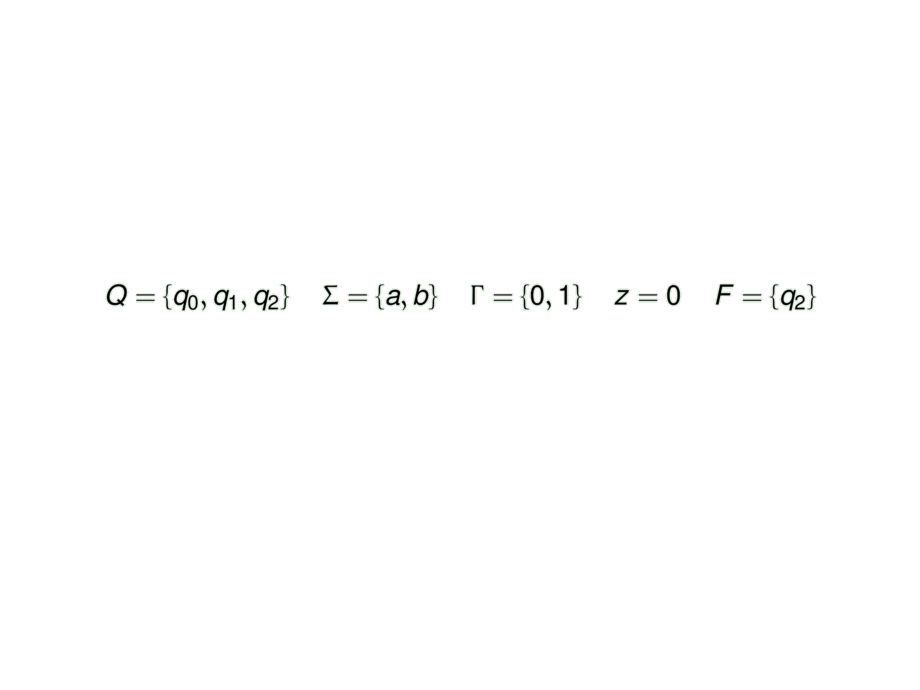
































































































25/162
\begin{frame}{Drawing Pushdown Automata}
\begin{goal}{}
The transition graph for a NPDA contains
\begin{talign}
\text{for every \quad \alert{$(q',v) \in \delta(q,\alpha,b)$} \quad}
\text{an arrow \quad \alert{$q \stackrel{\alpha[b/v]}{\longrightarrow} q'$}}
\end{talign}
\end{goal}
\pause
\begin{exampleblock}{}
We construct NPDA $M$ with $L(M) = \{\, a^n b^n \mid n \geq 0\, \}$.
\pause
\begin{talign}
Q &=\{q_0,q_1,q_2\} &
\Sigma &=\{a,b\} &
\Gamma &= \{0,1\} &
z &= 0 &
F &= \{q_2\}
\end{talign}
\pause
Intuition:
\begin{itemize}\setlength{\itemsep}{0pt}
\item In \alert{$q_0$} a stack \alert{$1^k0$} means: we have read $k$ $a$'s.
\item In \alert{$q_1$} a stack \alert{$1^k0$} means: we still have to read $k$ $b$'s.
\end{itemize}
\pause
\vspace{-1ex}
\begin{center}
\begin{tikzpicture}[default,node distance=25mm,->,s/.style={minimum size=5mm}]
\node (q0) [state,s] {$q_0$}; \draw ($(q0) + (-8mm,0mm)$) -- (q0);
\mpause[1]{\draw (q0) to[tloop] node [label,above] {$a[0/10]$} (q0);}
\mpause{\draw (q0) to[bloop] node [label,below] {$a[1/11]$} (q0);}
\mpause{\node (q1) [state,s,right of=q0] {$q_1$};}
\mpause{\draw (q0) to node [label,above] {$b[1/\lambda]$} (q1);}
\mpause{\draw (q1) to[tloop] node [label,above] {$b[1/\lambda]$} (q1);}
\mpause{\node (q2) [fstate,s,right of=q1] {$q_2$};}
\mpause{\draw (q1) to node [label,above] {$\lambda[0/\lambda]$} (q2);}
\mpause{\draw (q0) to[bend right=20] node [label,below] {$\lambda[0/\lambda]$} (q2);}
\end{tikzpicture}
\end{center}
\vspace{-1.5ex}
\end{exampleblock}
\bigskip
\end{frame}

