\begin{frame}{Removal of Unit Production Rules}
  \begin{block}{}
    A rule $A \to B$ is called \emph{unit production rule} (here $B \in V$).
  \end{block}
  \pause\medskip

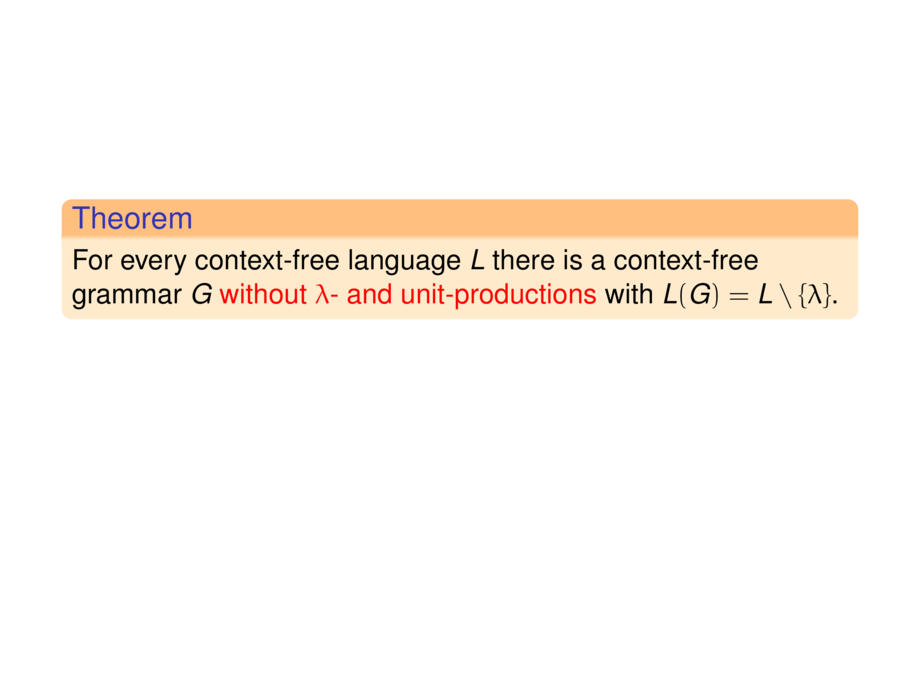
  \begin{goal}{Theorem}
    For every context-free language $L$ 
    there is a context-free grammar $G$ 
    \alert{without $\lambda$- and unit-productions} with $L(G) = L \setminus \{\lambda\}$.
  \end{goal}
  \pause
  
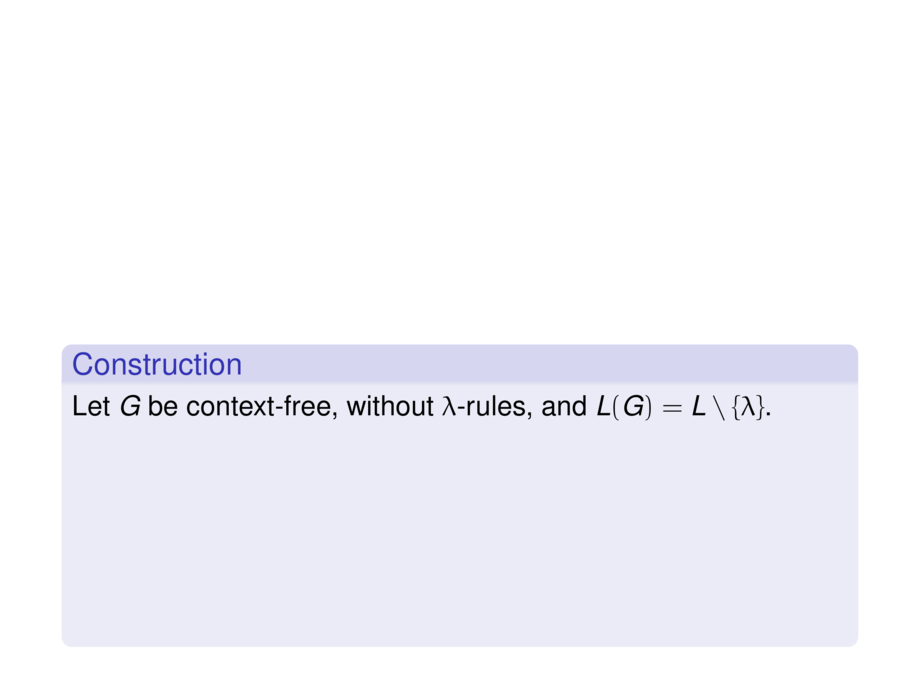
  \begin{construction}
    Let $G$ be context-free, without $\lambda$-rules, and $L(G) = L \setminus \{\lambda\}$.
    \begin{itemize}
    \pause
      \item 
        Determine all pairs $A \neq B$ with \alert{$A \Rightarrow^+ B$}.
    \pause
      \item 
        Whenever \alert{$A \Rightarrow^+ B$} and \alert{$B \to y$} is a rule, add a rule \alert{$A \to y$}.
    \pause
      \item 
        Remove all unit production rules.
    \end{itemize}
    \pause
    The resulting grammar $G$ has no $\lambda$- and unit-productions and 
    it has the property \alert{$L(G)= L \setminus \{\lambda\}$}.
  \end{construction}
\end{frame}