


































































































32/49
\begin{frame}{Ambiguous Grammars}
\begin{block}{}
A context-free grammar $G$ is \emph{ambiguous}
if there exists a word $w \in L(G)$ for which there are multiple derivation trees.
\end{block}
\pause\medskip
\begin{exampleblock}{}
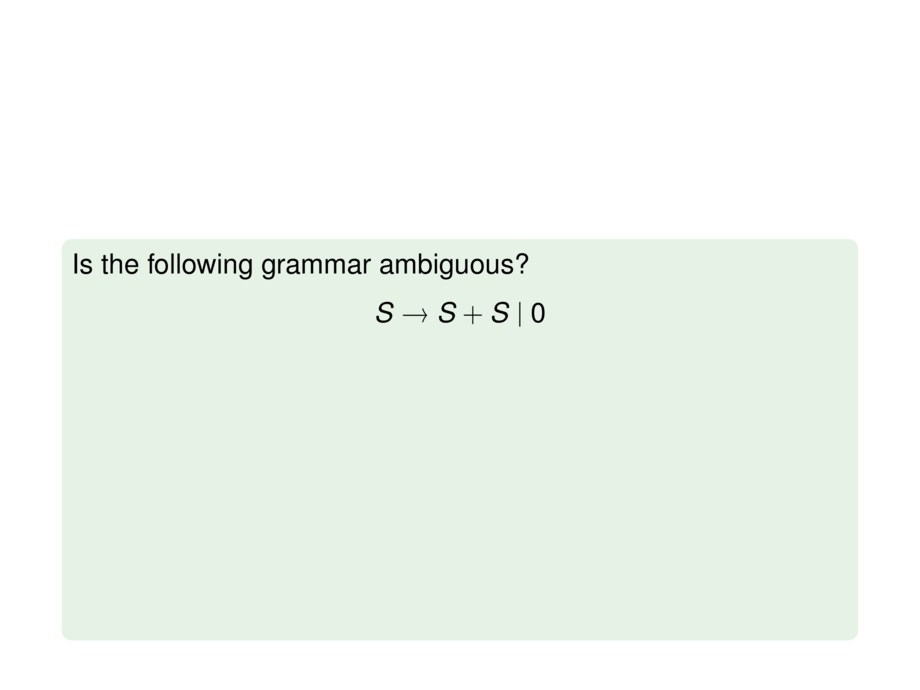
Is the following grammar ambiguous?
\begin{talign}
S \to S+S \mid 0
\end{talign}
\pause
Yes, there are two derivations trees for $0+0+0$:\pause
\begin{center}
\begin{tikzpicture}[default,>=latex,l/.style={yshift=-9mm},node distance=10mm,thin]
\node (1) {$S$};
\node (2a) [left of=1,l] {$S$};
\node (2b) [at=(1),l] {$+$};
\node (2c) [right of=1,l] {$S$};
\begin{scope}[node distance=6mm]
\node (3a) [left of=2a,l] {$S$};
\node (3b) [at=(2a),l] {$+$};
\node (3c) [right of=2a,l] {$S$};
\end{scope}
\node (3d) [at=(2c),l] {$0$};
\node (4a) [at=(3a),l] {$0$};
\node (4c) [at=(3c),l] {$0$};
\draw (1) to (2a);
\draw (1) to (2b);
\draw (1) to (2c);
\draw (2a) to (3a);
\draw (2a) to (3b);
\draw (2a) to (3c);
\draw (2c) to (3d);
\draw (3a) to (4a);
\draw (3c) to (4c);
\end{tikzpicture}
\hspace{1cm}
\begin{tikzpicture}[default,>=latex,l/.style={yshift=-9mm},node distance=10mm,thin]
\node (1) {$S$};
\node (2a) [left of=1,l] {$S$};
\node (2b) [at=(1),l] {$+$};
\node (2c) [right of=1,l] {$S$};
\node (3a) [at=(2a),l] {$0$};
\begin{scope}[node distance=6mm]
\node (3b) [left of=2c,l] {$S$};
\node (3c) [at=(2c),l] {$+$};
\node (3d) [right of=2c,l] {$S$};
\end{scope}
\node (4a) [at=(3b),l] {$0$};
\node (4c) [at=(3d),l] {$0$};
\draw (1) to (2a);
\draw (1) to (2b);
\draw (1) to (2c);
\draw (2a) to (3a);
\draw (2c) to (3b);
\draw (2c) to (3c);
\draw (2c) to (3d);
\draw (3b) to (4a);
\draw (3d) to (4c);
\end{tikzpicture}
\end{center}
\end{exampleblock}
\end{frame}

