\begin{frame}{Exercises (2)}
  \begin{exampleblock}{}
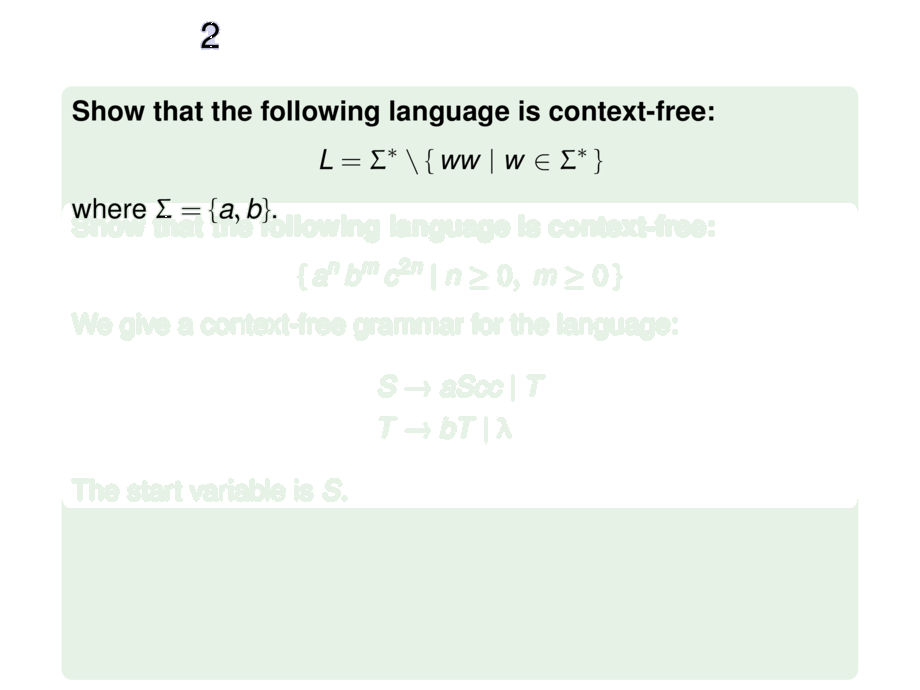
    \emph{Show that the following language is context-free:}
    \begin{talign}
      L = \Sigma^* \setminus \{\, ww \mid w \in \Sigma^* \,\}
    \end{talign}
    where $\Sigma = \{a,b\}$.
    \pause
    What shape do words $w \in L$ have?
    \begin{itemize}
    \pause
      \item $w$ has \emph{odd length}; \vspace{-.5ex}
    \pause
      \item $w$ has \emph{even length} such that \pause $w = uv$ with $|u| = |v|$ and \pause %\vspace{-.5ex}
        \begin{talign}
          u(m) \ne v(m)
        \end{talign}
        for some $0 \le m < |u|$. \pause Let $n = |u| - m-1$. Then $w$ is in 
        \begin{talign}
          \begin{aligned}
            &\,\Sigma^m \, \{\,a\,\} \, \Sigma^n \,\, \Sigma^m \, \{\,b\,\} \, \Sigma^n \\
            \cup\; &\underbrace{\Sigma^m \, \{\,b\,\} \, \Sigma^n}_{u} \, \underbrace{\Sigma^m \, \{\,a\,\} \, \Sigma^n}_{v}
          \end{aligned}
          \mpause[1]{
            && \raisebox{1.5ex}{$=$} &&
            \begin{aligned}
              &\,\Sigma^m \, \{\,a\,\} \, \Sigma^m \,\, \Sigma^n \, \{\,b\,\} \, \Sigma^n \\
              \cup\; &\underbrace{\Sigma^m \, \{\,b\,\} \, \Sigma^m}_{u} \, \underbrace{\Sigma^n \, \{\,a\,\} \, \Sigma^n}_{v}
            \end{aligned}
          }
        \end{talign}
    \end{itemize}
    \pause\pause\vspace{-.5ex}

    We give a context-free grammar for the language:
    \begin{talign}
      S &\to AB \mid BA \mpause[1]{\mid A \mid B} &
      A &\to XAX \mid a & X \to a \mid b\\
      &&
      B &\to XBX \mid b
    \end{talign}
  \end{exampleblock}
  \pause\bigskip
\end{frame}