
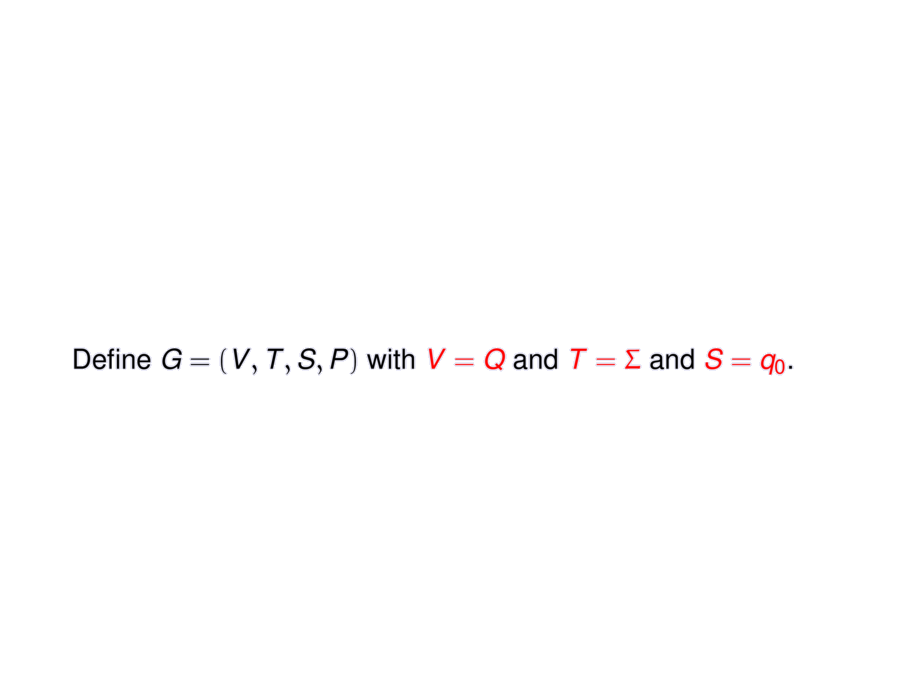
































































































62/80
\begin{frame}{From NFAs to Right Linear Grammars}
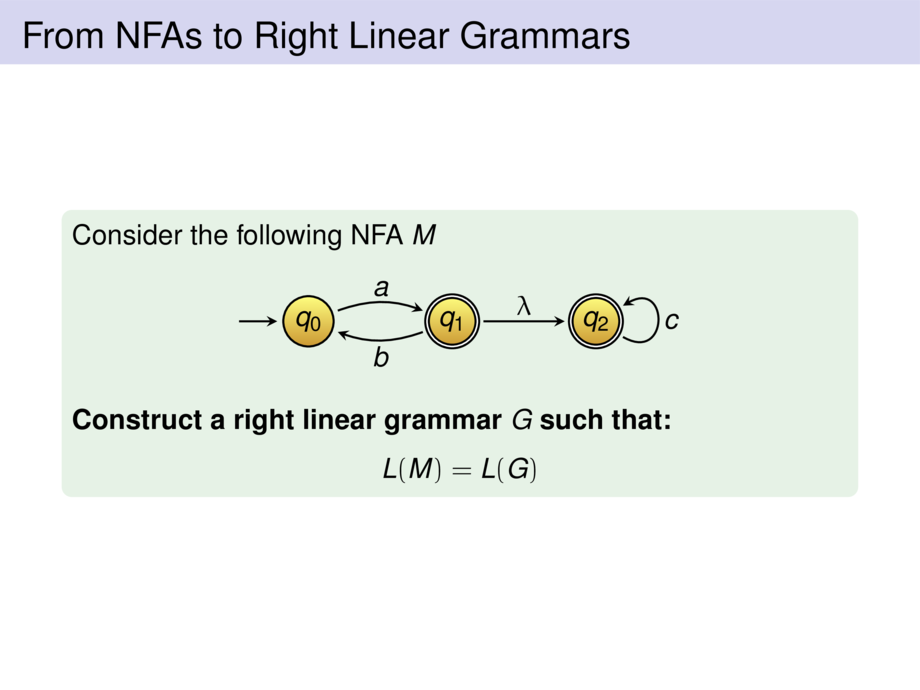
\begin{goal}{}
For every NFA $M$ there exists a right linear grammar $G$ with
\begin{talign}
L(G) = L(M)
\end{talign}
\end{goal}
\pause
\begin{construction}
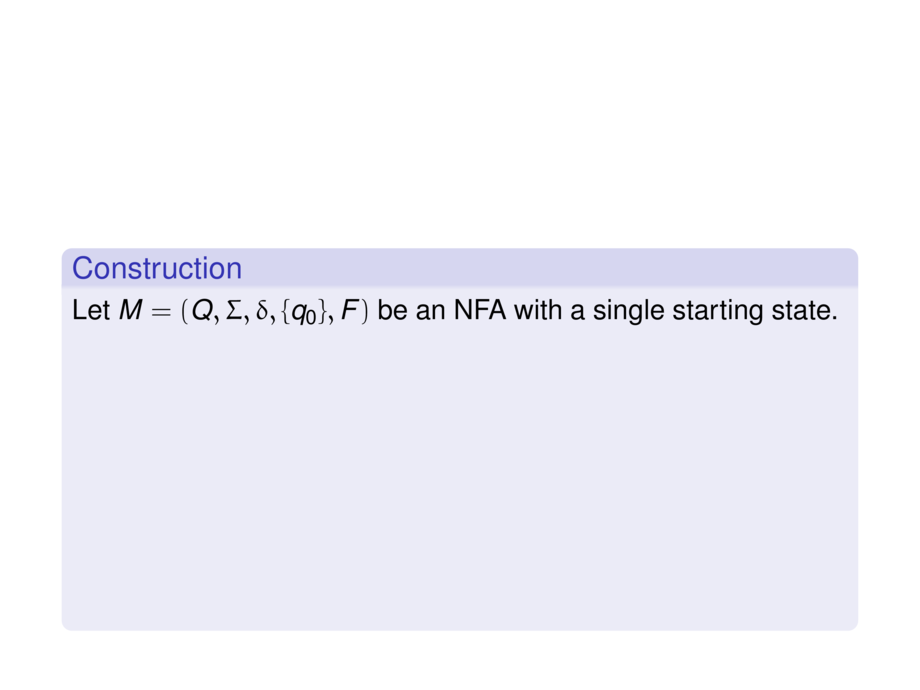
Let $M=(Q,\Sigma,\delta,\{q_0\},F)$ be an NFA with a single starting state.
\pause\medskip
Define $G=(V,T,S,P)$ with $\alert{V = Q}$ and $\alert{T = \Sigma}$ and $\alert{S = q_0}$.
\pause\medskip
The set \alert{$P$} consists of the following production rules
\begin{talign}
\alert{q} &\alert{\to \alpha q'} &&\text{for every $q' \in \delta(q,\alpha)$ where $\alpha \in \Sigma \cup \{\lambda\}$}\\
%\alert{q} &\alert{\to q'} &&\text{for every $q' \in \delta(q,\lambda)$}\\
\alert{q} &\alert{\to \lambda} &&\text{for every $q \in F$}
\end{talign}
\pause
Then: $A \Rightarrow^* uB$ in $G$ $\iff$ $A \apath{u} B$ in $M$.
\pause\medskip
It follows that, \alert{$L(G)=L(M)$}.
\end{construction}
\end{frame}

