\begin{frame}{From NFAs to Right Linear Grammars}
  \begin{exampleblock}{}
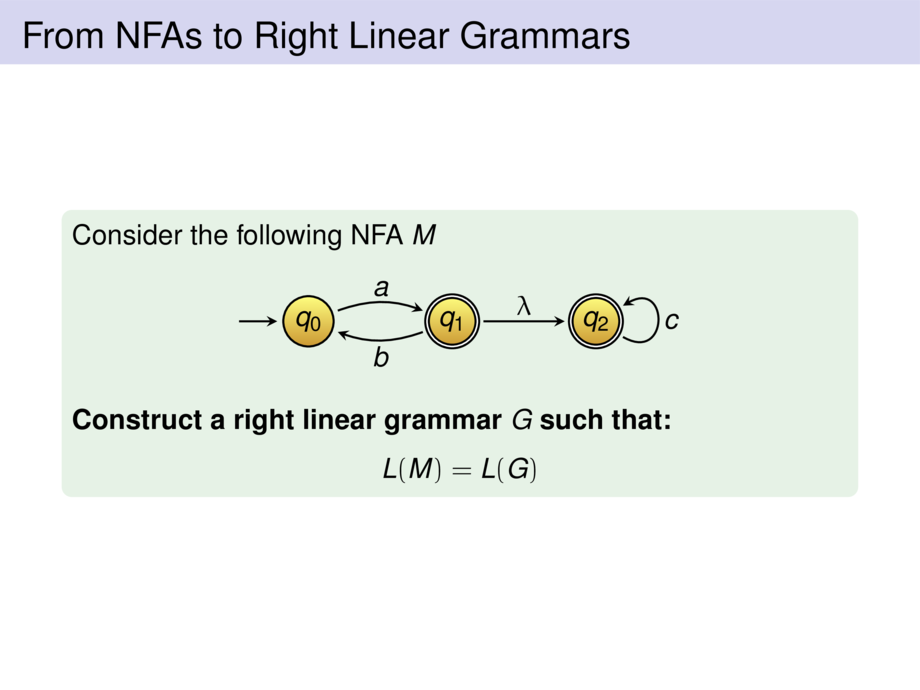
    Consider the following NFA $M$
    \begin{center}
      \begin{tikzpicture}[default,node distance=20mm,->]
        \node (q0) [state] {$q_0$}; \draw ($(q0) + (-10mm,0mm)$) -- (q0); 
        \node (q1) [fstate,right of=q0] {$q_1$};
        \node (q2) [fstate,right of=q1] {$q_2$};
        
        \draw (q0) to[bend left=20] node [label,above] {$a$} (q1);
        \draw (q1) to[bend left=20] node [label,below] {$b$} (q0);
        \draw (q1) to node [label,above] {$\lambda$} (q2);
        \draw (q2) to[rloop] node [label,right] {$c$} (q2);
      \end{tikzpicture}
    \end{center}
    \emph{Construct a right linear grammar $G$ such that:}
    \begin{talign}
      L(M) = L(G)
    \end{talign}
  \end{exampleblock}
\end{frame}