




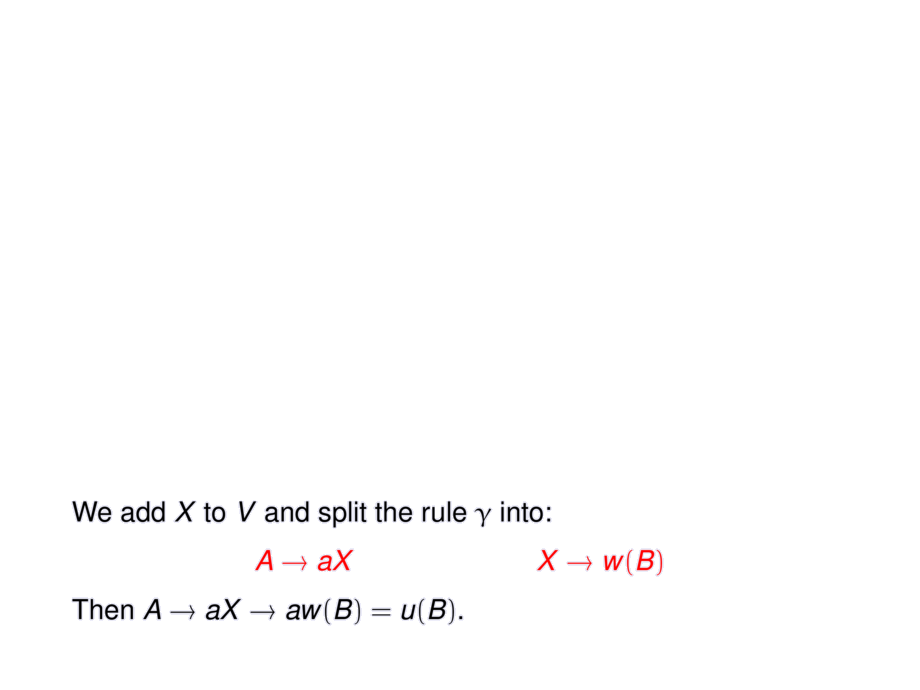





























































































55/80
\begin{frame}{(Strictly) Right Linear Grammars}
\begin{block}{Theorem}
Let $G$ be a right linear grammar $G$.
There exists a \emph{strictly} right linear grammar $H$ such that $L(G) = L(H)$.
\end{block}
\pause
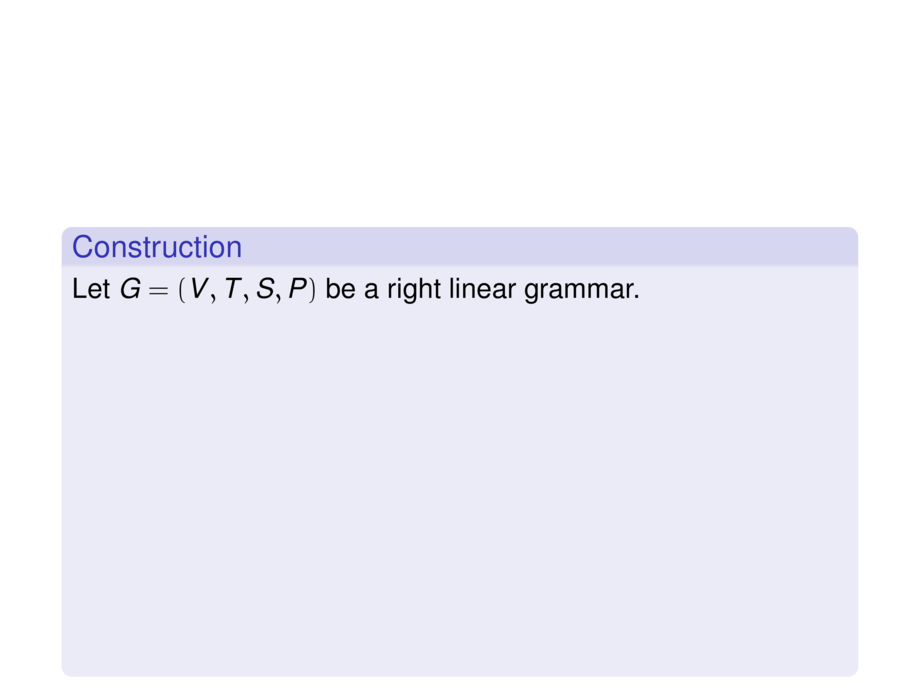
\begin{construction}
Let $G=(V,T,S,P)$ be a right linear grammar.
\pause\smallskip
Assume that we have a production rule $\gamma$ of the form
\begin{talign}
\alert{A \to u(B)}
\end{talign}
%with $A,B \in V$ and $u \in T^*$
with $\alert{|u| > 1}$.
\pause
Then \alert{$u = a w$} for some $a \in T$ and $w \in T^+$.
\pause\smallskip
Let \alert{$X$} be a \alert{fresh} variable ($X \not\in (V\cup T)$).
\pause\smallskip
We add $X$ to $V$ and split the rule $\gamma$ into:
\begin{talign}
\alert{A \to aX} && \alert{X \to w(B)}
\end{talign}
Then $A \to aX \to aw(B) = u(B)$. \pause It follows $L(G) = L(H)$.
\pause\smallskip
Repeat splitting until $|u| \le 1$ for all rules.
\end{construction}
\end{frame}

