\begin{frame}{NFAs Accepting Languages}
  \begin{block}{}
    The \emph{language accepted by} NFA $M = (Q,\Sigma,\delta,S,F)$ is
    \begin{talign}
      L(M) 
      &= \{\, w \in \Sigma^* \mid (q_0,w) \vdash^* (q,\lambda) \text{ with } q_0 \in S,\; q \in F \,\} \\
      &= \{\, w \in \Sigma^* \mid q_0 \apath{w} q \text{ with } q_0 \in S,\; q \in F \,\}
    \end{talign}
  \end{block}
  \pause

  \begin{center}
    \vspace{-.5ex}
    \input{tikz/nfa1.tex}
    \vspace{-1.5ex}
  \end{center}
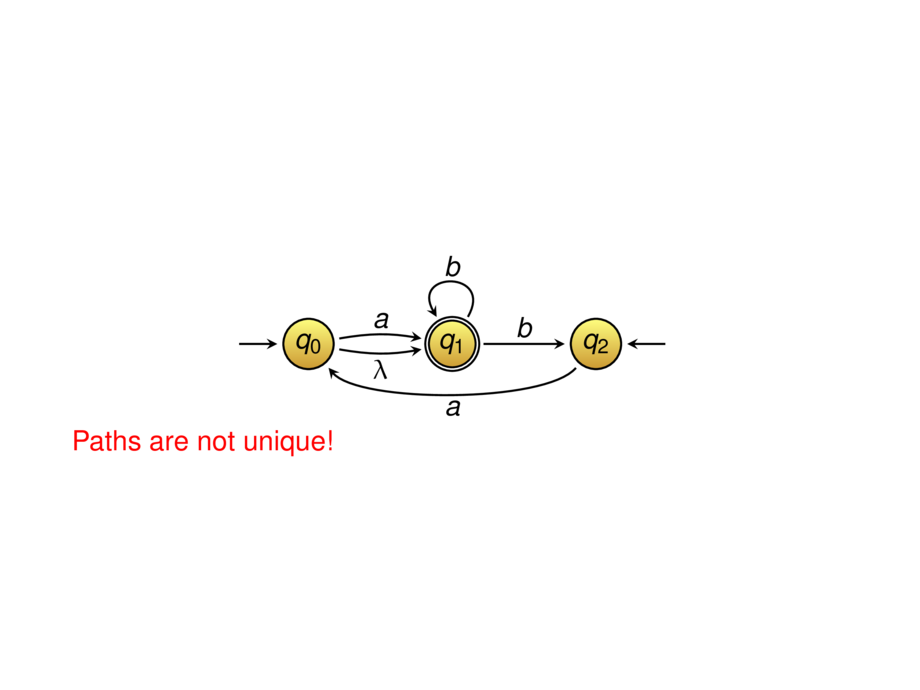
  \alert{Paths are not unique!}
  \pause
  Paths for input word $ab$:
  \pause
  \begin{talign}
    &(q_0,ab) \vdash (q_1,b) \vdash (q_1,\lambda) && \mpause[1]{\text{(ends in accepting state)}}\\
    &(q_0,ab) \vdash (q_1,b) \vdash (q_2,\lambda) \\
    &(q_2,ab) \vdash (q_0,b) \vdash (q_1,b) \vdash (q_1,\lambda) && \mpause[1]{\text{(ends in accepting state)}} \\
    &(q_2,ab) \vdash (q_0,b) \vdash (q_1,b) \vdash (q_2,\lambda)
  \end{talign}
  \pause
  \emph{One accepting path suffices!} 
  So $ab$ is accepted.
\end{frame}