


































































































67/87
\begin{frame}
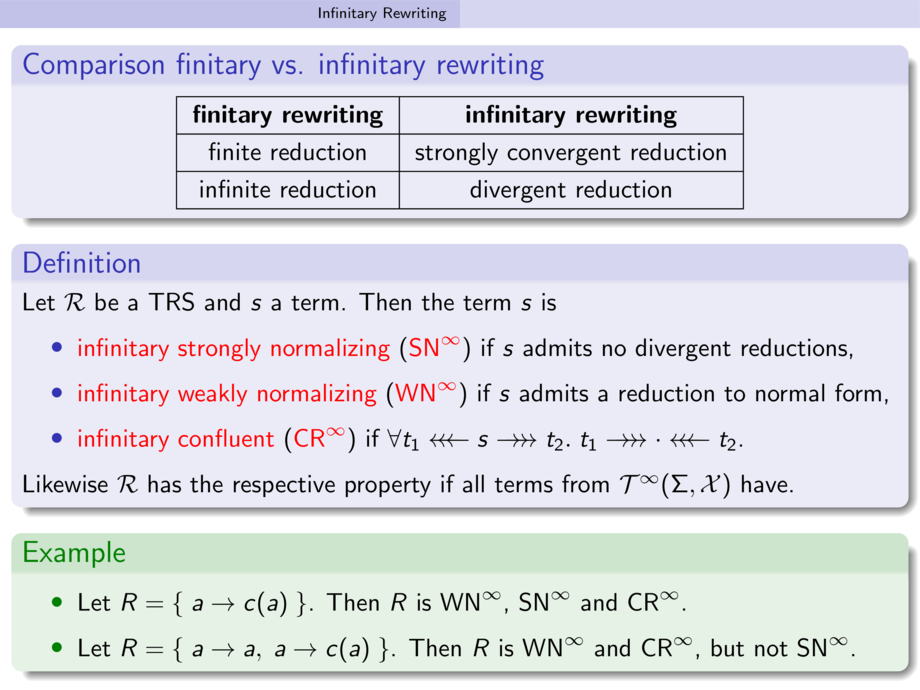
\begin{block}{Comparison finitary vs. infinitary rewriting}
\renewcommand{\arraystretch}{1.2}
\begin{center}
\begin{tabular}{|c|c|}
\hline
\textbf{finitary rewriting} & \textbf{infinitary rewriting} \\
\hline
finite reduction & strongly convergent reduction\\
\hline
infinite reduction & divergent reduction\\
\hline
\end{tabular}
\end{center}
\end{block}
\pause
\begin{definition}
Let $\atrs$ be a TRS and $s$ a term. Then the term $s$ is
\begin{itemize}
\item
\alert{infinitary strongly normalizing} (\alert{$\SNi$})
if $s$ admits no divergent reductions,
\item
\alert{infinitary weakly normalizing} (\alert{$\WNi$})
if $s$ admits a reduction to normal form,
\item
\alert{infinitary confluent} (\alert{$\CRi$})
if $\forall t_1 \iredi s \ired t_2.\; t_1 \ired \cdot \iredi t_2$.
\end{itemize}
Likewise $\atrs$ has the respective property if all terms from $\iter$ have.
\end{definition}
\pause
\begin{example}
\begin{itemize}
\item Let $R = \{\;a \to c(a)\;\}$. \pause Then $R$ is $\WNi$, $\SNi$ and $\CRi$.
\pause
\item Let $R = \{\;a \to a,\; a \to c(a)\;\}$. \pause Then $R$ is $\WNi$ and $\CRi$, but not $\SNi$.
\end{itemize}
\end{example}
\end{frame}

