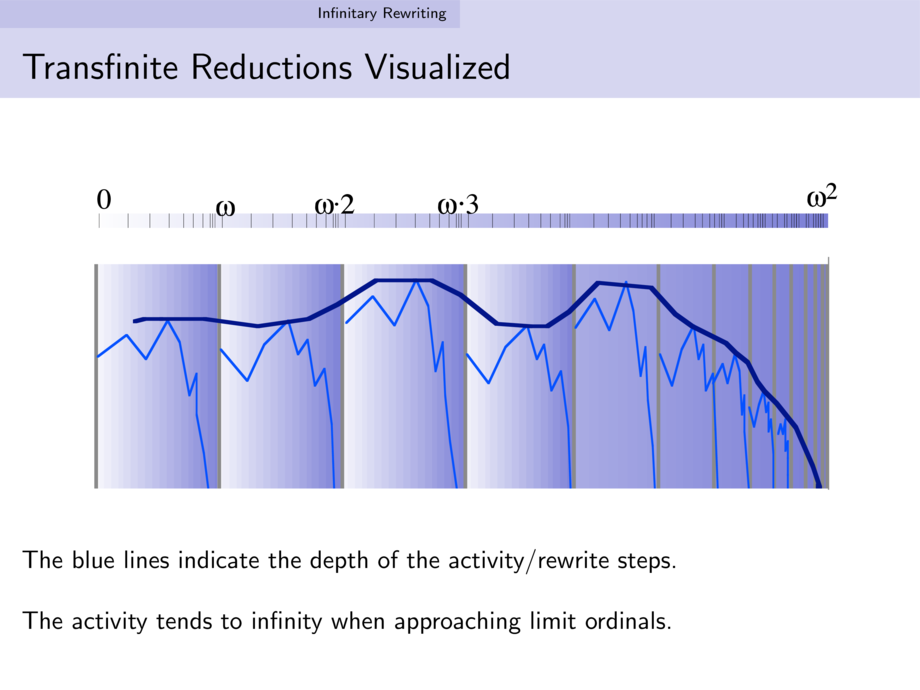



































































































47/87
\begin{frame}
\frametitle{Why more than Cauchy-convergence?}
We consider the TRS:
\begin{align*}
f(x,y) &\to f(y,x)\\
a &\to b
\end{align*}
\pause
We start from $f(a,a)$ and trace the left occurrence of $a$:
\pause
\begin{align*}
f(\overline{a},a) \to f(a,\overline{a}) \to f(\overline{a},a) \to f(a,\overline{a}) \to^\omega \alert{\ ?}
\end{align*}
\vspace{-2ex}
The rewrite sequence without overlining is Cauchy-convergent.
\medskip
However, what are the residuals of the left $a$ after $\omega$-many steps?
\pause\medskip
Although it appears as if the term has a limit, this is only a syntactic accident.\\
The subterms get swapped all the time\ldots
\end{frame}

