\begin{frame}
  \frametitle{Ordinals}

  \begin{definition}
  For ordinals $\alpha$, we define $\alpha^+ = \alpha \cup \{\alpha\}$, the \alert{successor of $\alpha$}.
  \medskip
  
  \onslide<2->{
  An ordinal $\alpha$ is a \alert{successor} ordinal if $\alpha = \beta^+$
  for some ordinal $\beta$.
  }
  \medskip

  \onslide<3->{
  If $\alpha \ne 0$ and $\alpha$ is not a successor ordinal,
  then $\alpha$ is called \alert{limit} ordinal.
  }
  \end{definition}
  
  \onslide<1->{
  \begin{center}
    \begin{tikzpicture}
      \vordinal{20}{30}
    \end{tikzpicture}
  \end{center}
  }
  
  \onslide<2->{
  \begin{example}
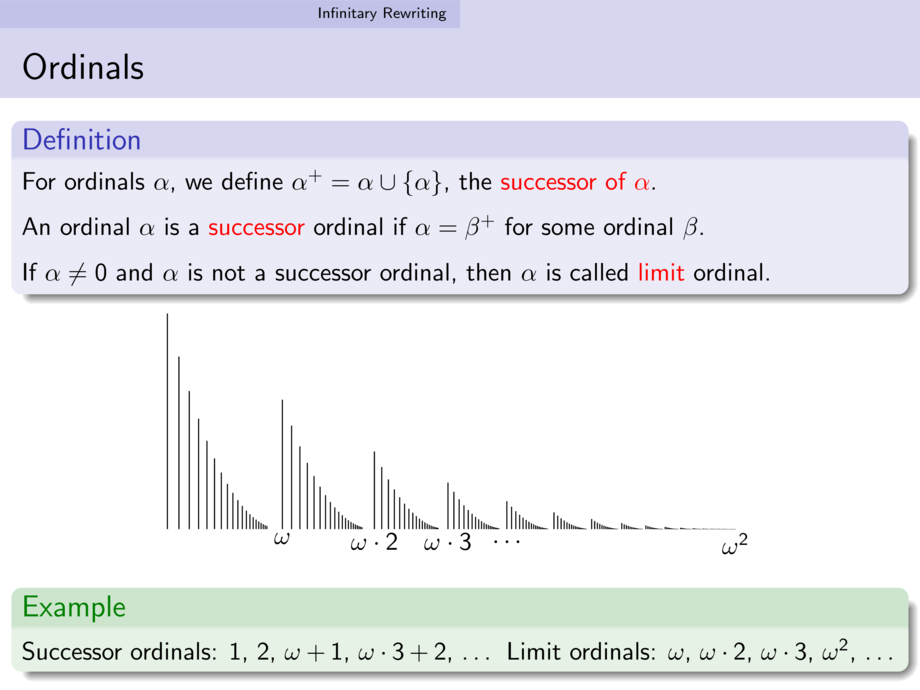
  Successor ordinals: $1$, $2$, $\omega+1$, $\omega\cdot 3 + 2$, \ldots
  \hfill
  \onslide<3->{
  Limit ordinals: $\omega$, $\omega\cdot 2$, $\omega \cdot 3$, $\omega^2$, \ldots
  }
  \end{example}
  }
\end{frame}