\begin{frame}
  \frametitle{Infinite Terms}
  
  \begin{center}
    \begin{tikzpicture}[level distance=6mm,inner sep=0.5mm,sibling distance=10mm]
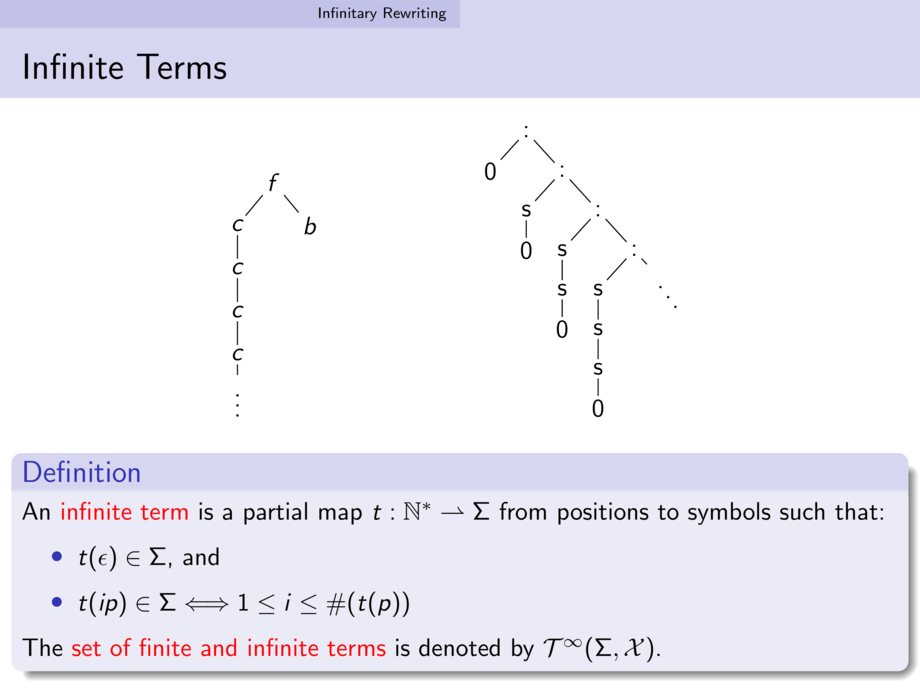
    \node {$f$}
      child { node {$c$} 
        child { node {$c$} 
          child { node {$c$} 
            child { node {$c$} 
              child { node {$\vdots$} 
              }
            }
          }
        }
      }
      child { node {$b$} 
      };
    \end{tikzpicture}
    \hspace{2cm}
    \begin{tikzpicture}[level distance=5.5mm,inner sep=0.5mm,sibling distance=10mm]
    \node {$\sstrcns$}
      child { node {$0$} }
      child { node {$\sstrcns$}
        child { node {$\msf{s}$} child { node {$0$} } }
        child { node {$\sstrcns$}
          child { node {$\msf{s}$} child { node {$\msf{s}$} child { node {$0$} } } }
          child { node {$\sstrcns$}
            child { node {$\msf{s}$} child { node {$\msf{s}$} child { node {$\msf{s}$} child { node {$0$} } } } }
            child { node {\rotatebox{-15}{$\ddots$}}
            }
          }
        }
      };
    \end{tikzpicture}
  \end{center}
  
  \begin{definition}
  An \alert{infinite term} is a partial map $t : \NN^* \pto \Sigma$ from positions to symbols such that:
  \begin{itemize}
    \item $t(\epsilon) \in \Sigma$, and
    \item $t(i p) \in \Sigma \Longleftrightarrow 1 \le i \le \arity{t(p)}$
  \end{itemize}
  \pause
  The \alert{set of finite and infinite terms} is denoted by $\iter$.
  \end{definition}
\end{frame}