\begin{frame}[label=tower]
  \small
  
  \begin{center}
  \newcommand{\mdown}{-.6cm}
  \begin{tikzpicture}[node distance=20mm,thick,>=stealth]
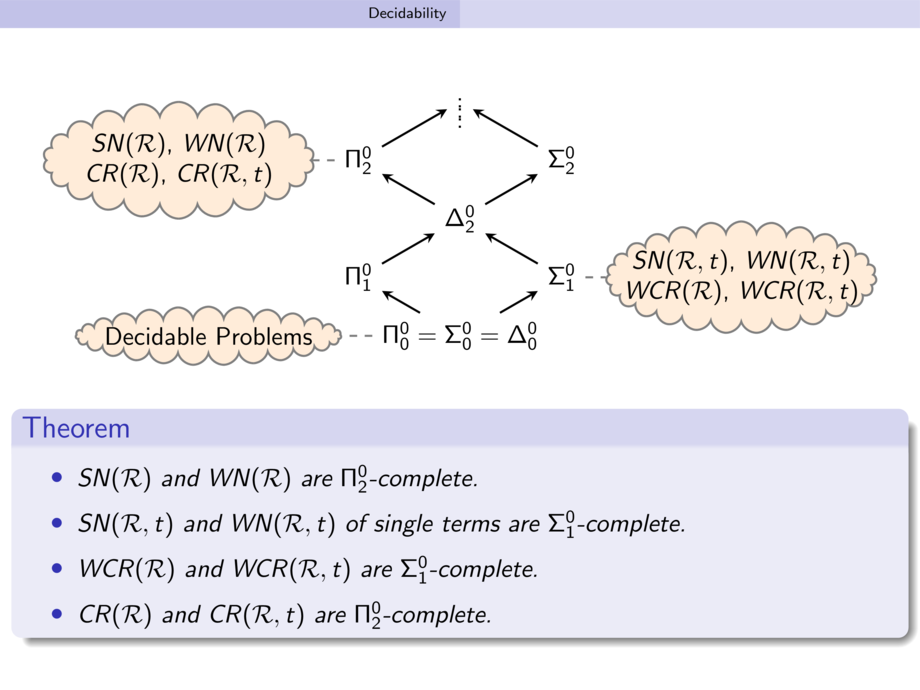
  \node (d00) {$\cpi{0}{0} = \csig{0}{0} = \cdel{0}{0} $};
  \node (p01) [above left of=d00,yshift=\mdown] {$\cpi{0}{1}$}; \draw [->] (d00) -- (p01);
  \node (s01) [above right of=d00,yshift=\mdown] {$\csig{0}{1}$}; \draw [->] (d00) -- (s01);
  \node (d02) [above right of=p01,yshift=\mdown] {$\cdel{0}{2}$}; \draw [->] (p01) -- (d02); \draw [->] (s01) -- (d02);
  \node (p02) [above left of=d02,yshift=\mdown] {${\cpi{0}{2}}$}; \draw [->] (d02) -- (p02);
  \node (s02) [above right of=d02,yshift=\mdown] {$\csig{0}{2}$}; \draw [->] (d02) -- (s02);
  \node (d03) [above right of=p02,yshift=\mdown] {$\vdots$}; \draw [->] (p02) -- (d03); \draw [->] (s02) -- (d03);
  \node (d04) [above of=d03,node distance=5mm,yshift=\mdown] {$\vdots$};

  \begin{scope}[draw=black!50]
  \node (fr) [node distance=20mm,left of=p02,xshift=-5mm,cloud,cloud puffs=22,draw,cloud ignores aspect,fill=orange!15,inner sep=.5mm] 
             {\parbox{2.5cm}{\centerline{$SN(\atrs)$, $WN(\atrs)$}\centerline{$CR(\atrs)$, $CR(\atrs,t)$}}};
  \draw [dashed] (p02) -- (fr);

  \node (psf) [node distance=20mm,right of=s01,yshift=0mm,xshift=5mm,cloud,cloud puffs=27,draw,cloud ignores aspect,fill=orange!15,inner sep=.5mm] 
             {\parbox{2.5cm}{\centerline{$SN(\atrs,t)$, $WN(\atrs,t)$}\centerline{$WCR(\atrs)$, $WCR(\atrs,t)$}}};
  \draw [dashed] (s01) -- (psf);


  \node (psf) [node distance=20mm,left of=d00,xshift=-15mm,cloud,cloud puffs=27,draw,cloud ignores aspect,fill=orange!15,inner sep=.5mm] 
             {\parbox{2.5cm}{\centerline{Decidable Problems}}};
  \draw [dashed] (d00) -- (psf);
  \end{scope}
  \end{tikzpicture}
  \end{center}

  \begin{theorem}
  \begin{itemize}
    \item $SN(\atrs)$ and $WN(\atrs)$ are $\cpi{0}{2}$-complete.
    \item $SN(\atrs,t)$ and $WN(\atrs,t)$ of single terms are $\csig{0}{1}$-complete.
    \item $WCR(\atrs)$ and $WCR(\atrs,t)$ are $\csig{0}{1}$-complete.
    \item $CR(\atrs)$ and $CR(\atrs,t)$ are $\cpi{0}{2}$-complete.
  \end{itemize}
  \end{theorem}

%   \begin{theorem}
%   On the input of terms $t$, $u$, the following properties
%   \begin{itemize} 
%   \item {\em reduction} ($t \to^* u$), 
%   \item {\em joinability} ($t \to^* \cdot \FromP{*} u$), and
%   \item {\em conversion} ($t \conv u$) 
%   \end{itemize}
%   are all $\csig{0}{1}$-complete.
%   \end{theorem}
\end{frame}