\begin{frame}
  \small
  
  \begin{definition}
  A \alert{Turing machine} is a tuple $\langle Q, q_0, F, \Sigma, \Box, \delta \rangle$ where:
  \begin{itemize}
    \item $Q$ is a finite set of states,
    \item $q_0 \in Q$ is the initial state,
    \item $F \subseteq Q$ is the set of final states,
    \item $\Sigma$ is a finite alphabet,
    \item $\Box \in \Sigma$ is the blank symbol,
    \item $\delta : (Q \setminus F) \times \Sigma \to Q \times \Sigma \times \{L,R\}$ is the \alert{transition function}.
  \end{itemize}
  \end{definition}
  \medskip\pause
  
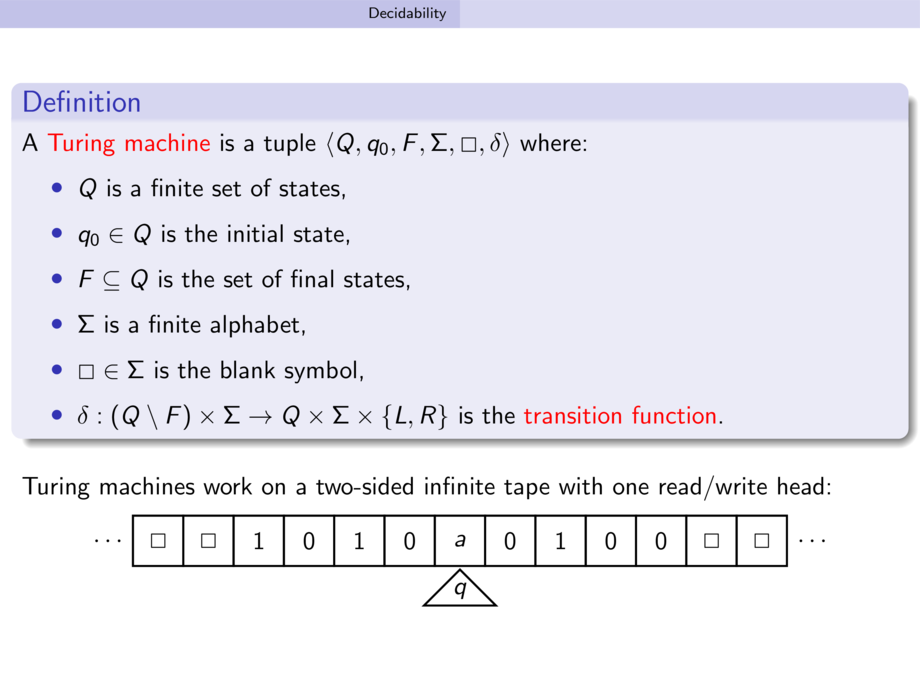
  Turing machines work on a two-sided infinite tape with one read/write head:
  
  \turing{\Box,\Box,1,0,1,0,a,0,1,0,0,\Box,\Box}{q}{0}
\end{frame}