


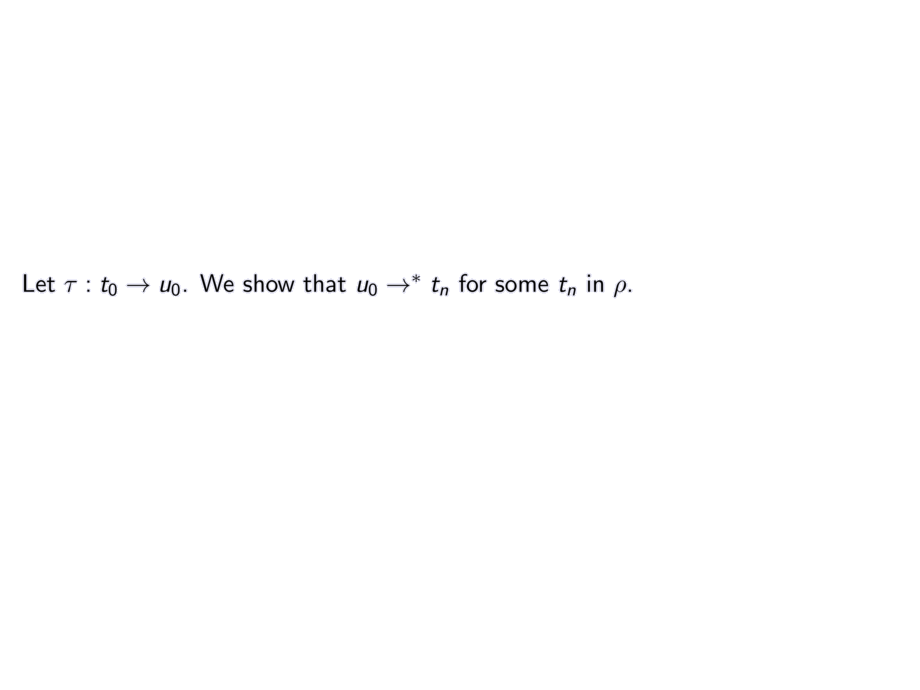































































































135/143
\begin{frame}
\small
\begin{theorem}
For orthogonal TRSs, every fair strategy is cofinal.
\end{theorem}
\pause
\begin{proof}
Let $\rho : t_0 \to t_1 \to \ldots$ be a fair rewrite sequence.
\medskip\pause
Let $\tau : t_0 \to u_0$. We show that $u_0 \to^* t_n$ for some $t_n$ in $\rho$.
\pause
\begin{center}
\begin{tikzpicture}[thick,node distance=20mm]
\node (s1) {$u_0$};
\node [right of=s1] (s2) {$u_1$};
\node [right of=s2] (s3) {$u_2$};
\node [right of=s3] (sd) {$\ldots$};
\node [right of=sd] (sn) {$u_n$};
\node [above of=s1,node distance=10mm] (t1) {$t_0$};
\node [right of=t1] (t2) {$t_1$};
\node [right of=t2] (t3) {$t_2$};
\node [right of=t3] (td) {$\ldots$};
\node [right of=td] (tn) {$t_n$};
\node [right of=tn] (ti) {$\ldots$};
\begin{scope}[->]
\draw (t1) -- (t2);
\draw (t2) -- (t3);
\draw (t3) -- (td);
\draw (td) -- (tn);
\draw (tn) -- (ti);
\draw (t1) -- (s1) node [midway,right] {$\tau$};
\end{scope}
\begin{scope}[->>]
\draw (s1) -- (s2);
\draw (s2) -- (s3);
\draw (s3) -- (sd);
\draw (sd) -- (sn);
\draw (t2) -- (s2) node [midway,right] {$\tau\project\rho_1$};
\draw (t3) -- (s3) node [midway,right] {$\tau\project\rho_2$};
\end{scope}
\draw (tn) -- (sn) node [midway,right] {$\varnothing$};
\end{tikzpicture}
\end{center}
\vspace{-2ex}
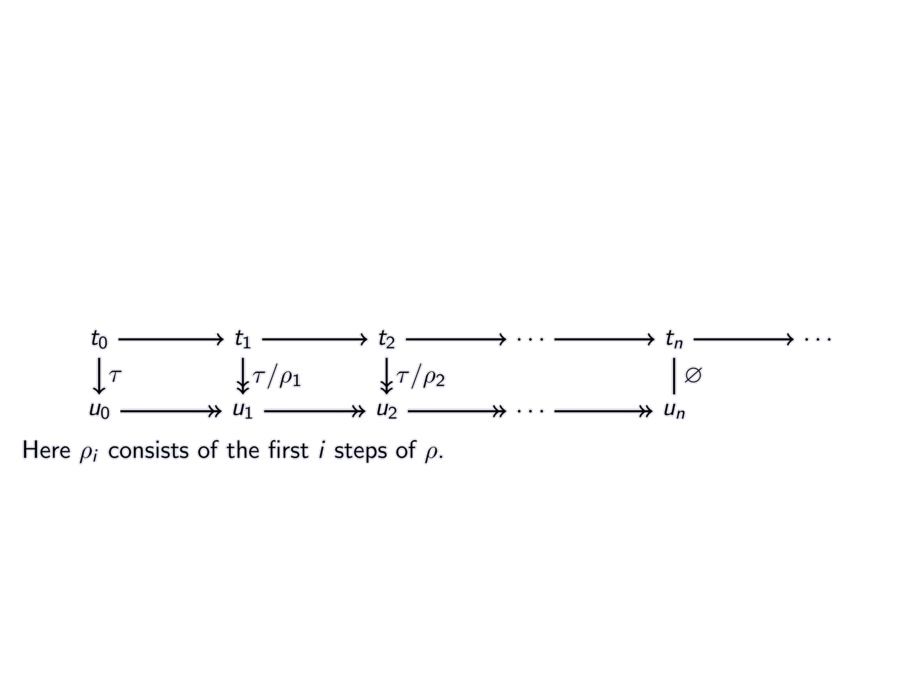
Here $\rho_i$ consists of the first $i$ steps of $\rho$.
\medskip\pause
By fairness of $\rho$ there exists $n$ such that $\tau \project \rho_n = \varnothing$.
\pause
Hence $u_n = t_n$ and $u_0 \to^* t_n$.
\medskip\pause
The reduction $u_0 \to u_1 \to \ldots \to u_n \to t_{n+1} \to t_{n+2}$ is fair again.\\
(every redex occurrence in $t_n$ is eventually secured)
\medskip\pause
By induction over the length of $t_0 \to^* u_0$ we get $u_0 \to^* t_n$ for some $t_n$ in $\rho$.
\end{proof}
\end{frame}

