
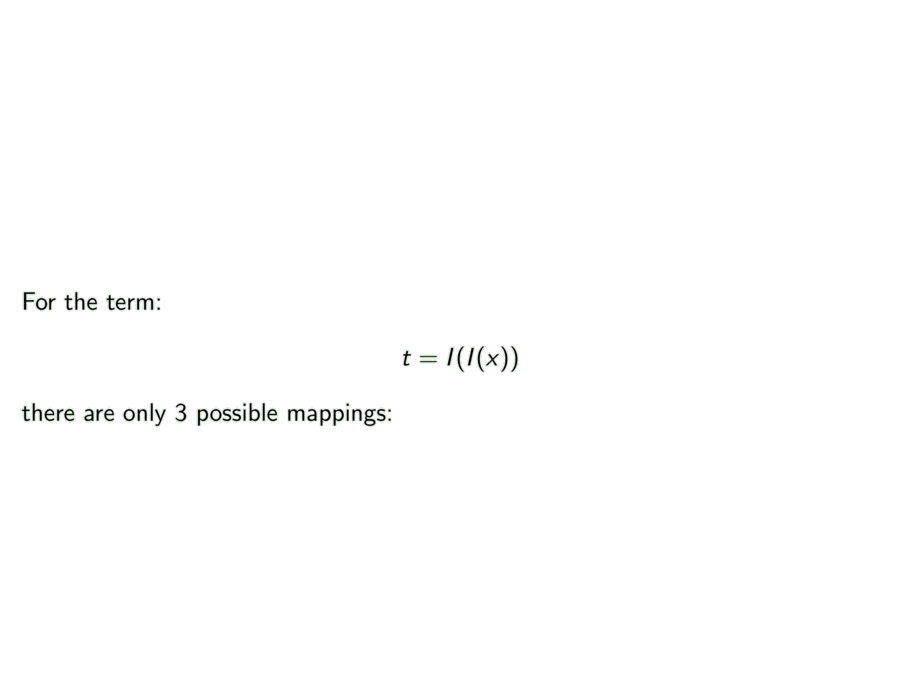

































































































17/143
\begin{frame}
\small
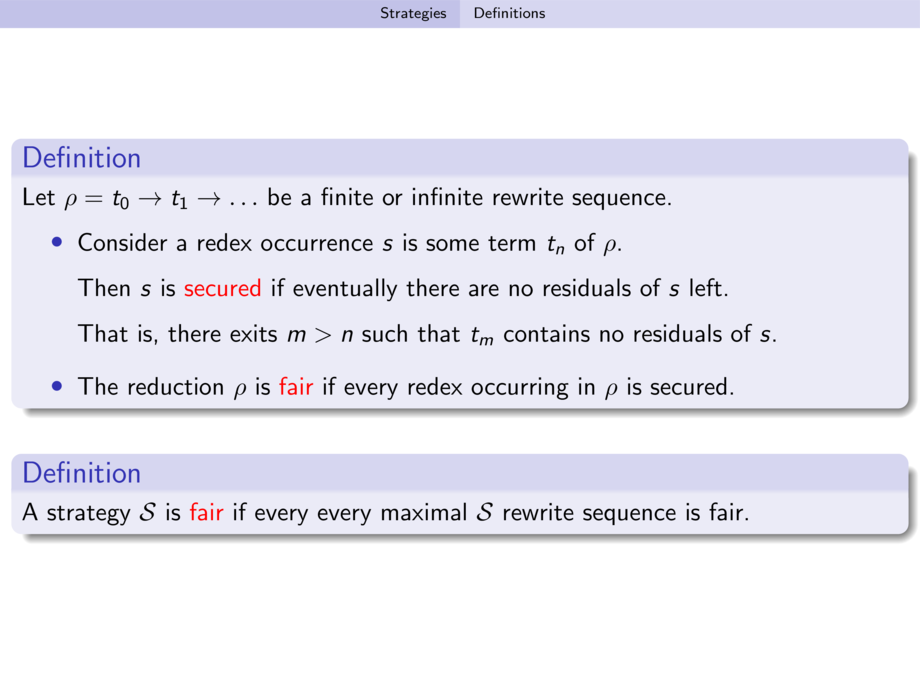
\begin{definition}
A \alert{one-step} strategy maps every reducible term to a set of one-step reductions.
\end{definition}
\begin{example}
There exists no fair one-step strategy for $\atrs = \{I(x) \to I(x)\}$.
\medskip\pause
For the term:
\begin{align*}
t = I(I(x))
\end{align*}
there are only 3 possible mappings:
\begin{itemize}
\pause
\item $\SS(t) = \{\alert{I}(I(x)) \to_{\varepsilon} I(I(x))\}$,
\pause
\item $\SS(t) = \{I(\alert{I}(x)) \to_{1} I(I(x))\}$, or
\pause
\item $\SS(t) = \{\alert{I}(I(x)) \to_{\varepsilon} I(I(x)), \; I(\alert{I}(x)) \to_1 I(I(x))\}$.
\end{itemize}
\pause
None of these is fair as we can always continue to reduce the same occurrence of $I$.
\end{example}
\end{frame}

