\begin{frame}
  \small
  
  \begin{definition}
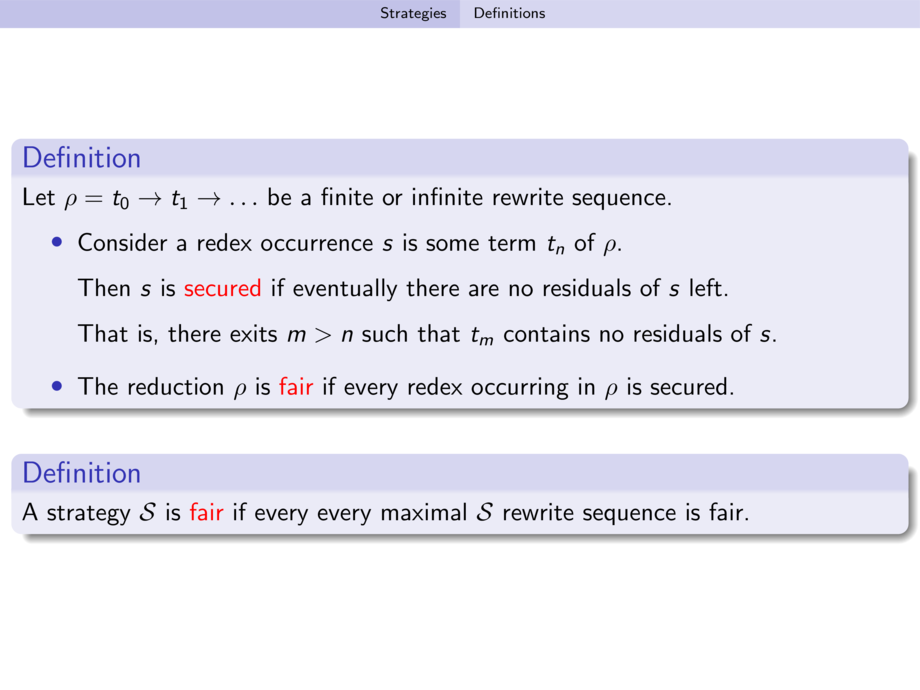
  Let $\rho = t_0 \to t_1 \to \ldots$ be a finite or infinite rewrite sequence.
  \begin{itemize}
  \pause
    \item Consider a redex occurrence $s$ is some term $t_n$ of $\rho$.
          \smallskip\pause
          
          Then $s$ is \alert{secured} if eventually there are no residuals of $s$ left.
          \smallskip\pause
          
          That is, there exits $m > n$ such that $t_m$ contains no residuals of $s$.       
          \smallskip
  \pause
    \item The reduction $\rho$ is \alert{fair} if every redex occurring in $\rho$ is secured.
  \end{itemize}
  \end{definition}
  \medskip\pause
  
  \begin{definition}
  A strategy $\SS$ is \alert{fair} if every every maximal $\SS$
  rewrite sequence is fair.
  \end{definition}
\end{frame}