\begin{frame}
  \small
  
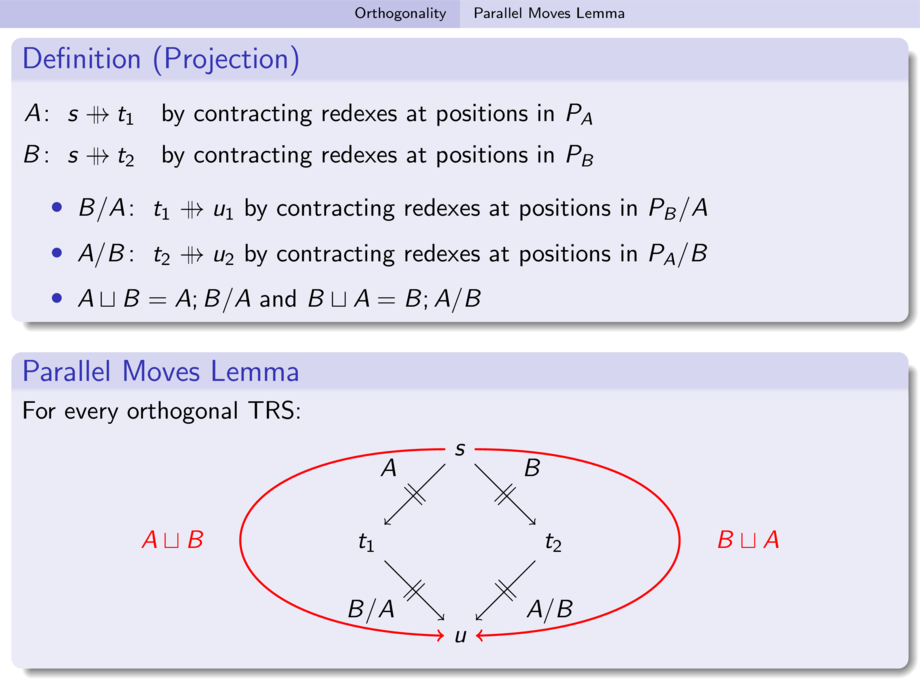
  \begin{definition}
  \smallskip
  $A\colon s_1 \to^* t_1$ and $B\colon s_2 \to^* t_2$
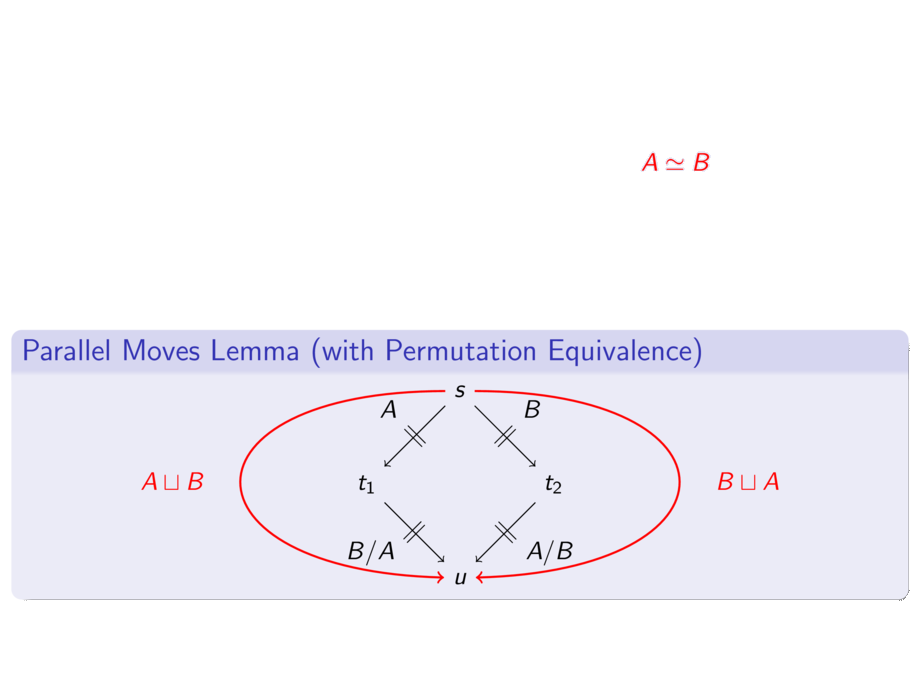
  are \alert{permutation equivalent} ($\alert<2>{A \simeq B}$) if
  \begin{enumerate}
  \item ~
  $s_1 = s_2$
  \vspace{-1ex}
  \item ~
  $t_1 = t_2$
  \vspace{-1ex}
  \item ~
  $p \project A = p \project B$ for all redex positions $p$ in $s_1$
  \end{enumerate}
  \end{definition}

%   \pause
%   \begin{definition}
%   $A\colon s \to^* t_1$ and $B\colon s \to^* t_2$ are \alert{permutation equivalent} ($\alert{A \simeq B}$)if \
%   $$ A \project B = \varnothing \text{ and } B \project A = \varnothing$$
%   \end{definition}

  \pause
  \begin{block}{Parallel Moves Lemma (with Permutation Equivalence)}
  \vspace{-1.5ex}
  \begin{center}
  \begin{tikzpicture}[on grid,baseline=(1).baseline]
  \node (1)              {$\strut s$};
  \onslide<3->{
  \node (c) [below=of 1] {$\alert<3>{\simeq}$};
  }
  \node (2) [left=of c]  {$t_1$};
  \node (3) [right=of c] {$t_2$};
  \draw[->] (1) -- (2) node[midway,sloped] {$\|$};
  \draw[->] (1) -- (3) node[midway,sloped] {$\|$};
  \node (6) at (-1.0,-0.25) {$A$};
  \node (7) at (1.0,-0.25)  {$B$};
  \node (4) [below=of c] {$\strut u$};
  \draw[->] (2) -- (4) node[midway,sloped] {$\|$};
  \draw[->] (3) -- (4) node[midway,sloped] {$\|$};
  \node (8) at (-1.25,-2.25) {$B \project A$};
  \node (9) at (1.25,-2.25)  {$A \project B$};
  \draw[->,thick,red] (1) .. controls (-4,0) and (-4,-2.5) .. (4);
  \draw[->,thick,red] (1) .. controls (4,0) and (4,-2.5) .. (4);
  \node at (-4,-1.25) {$\alert{A \sqcup B}$};
  \node at (4,-1.25) {$\alert{B \sqcup A}$};
  \end{tikzpicture}
  \end{center}
  \vspace{-3ex}
  \end{block}
\end{frame}