\begin{frame}
  \small
  
  \begin{lemma}
  \smallskip
  Every orthogonal TRS is locally confluent.
  \end{lemma}
  \pause
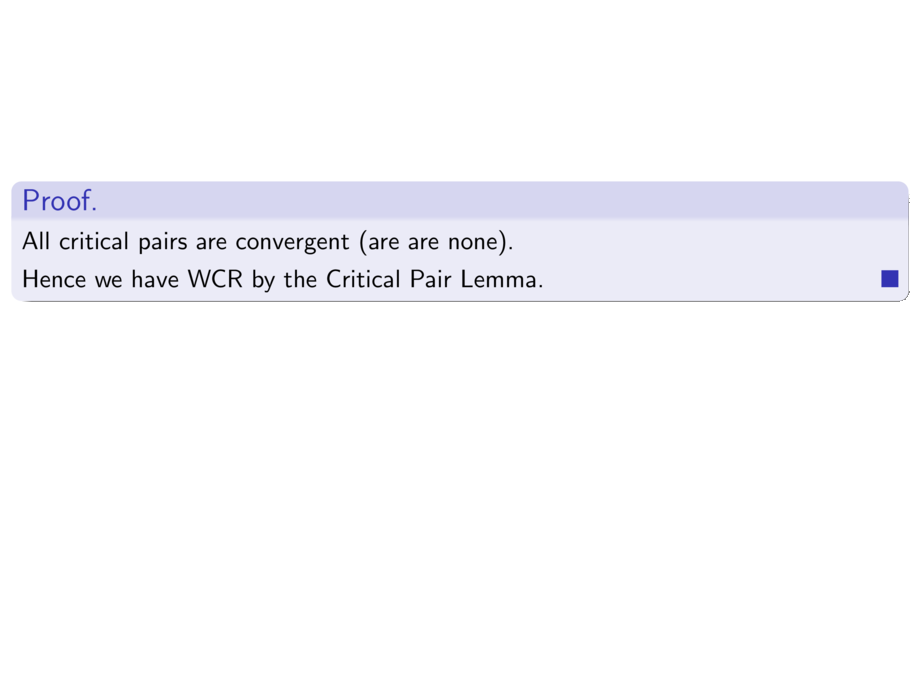
  \begin{proof}
  All critical pairs are convergent (are are none).
  \smallskip
  
  Hence we have WCR by the Critical Pair Lemma.
  \end{proof}
  \medskip\pause

  \begin{theorem}
  \smallskip
  Every orthogonal TRS is \alert<1>{confluent} \\[-3ex]
  \[
  \qquad\qquad\qquad\begin{tikzpicture}[on grid,baseline=(1).baseline]
  \node (1)                    {$\strut s$};
  \node (2) [below left=of 1]  {$t$};
  \node (3) [below right=of 1] {$u$};
  \node (4) [below right=of 2] {$\strut \alert<2>{v}$};
  \node (5) [left=of 1] {\makebox[3cm][l]{$\strut\forall s,t,u$}};
  \node (6) [left=of 4] {\makebox[3cm][l]{$\strut\alert<2>{\exists v}$}};
  \draw[->>]        (1) -- (2); % node[midway,sloped,above] {${}_*$};
  \draw[->>]        (1) -- (3); % node[midway,sloped,above] {${}_*$};
  \draw[dotted,->>] (2) -- (4); % node[midway,sloped,below] {${}^*$};
  \draw[dotted,->>] (3) -- (4); % node[midway,sloped,below] {${}^*$};
  \end{tikzpicture}
  \]
  \end{theorem}
  \pause
  
  For orthogonal TRSs there is a canonical way to compute common reduct\ldots
\end{frame}