\begin{frame}[t]
  \frametitle{Case (b) and (b'): Nested redexes}

  \begin{minipage}{.5\textwidth}
  \includegraphics[width=.90\textwidth]{../graphics/critpairlemma}\\[3ex]
  \end{minipage}
  \begin{minipage}{.49\textwidth}
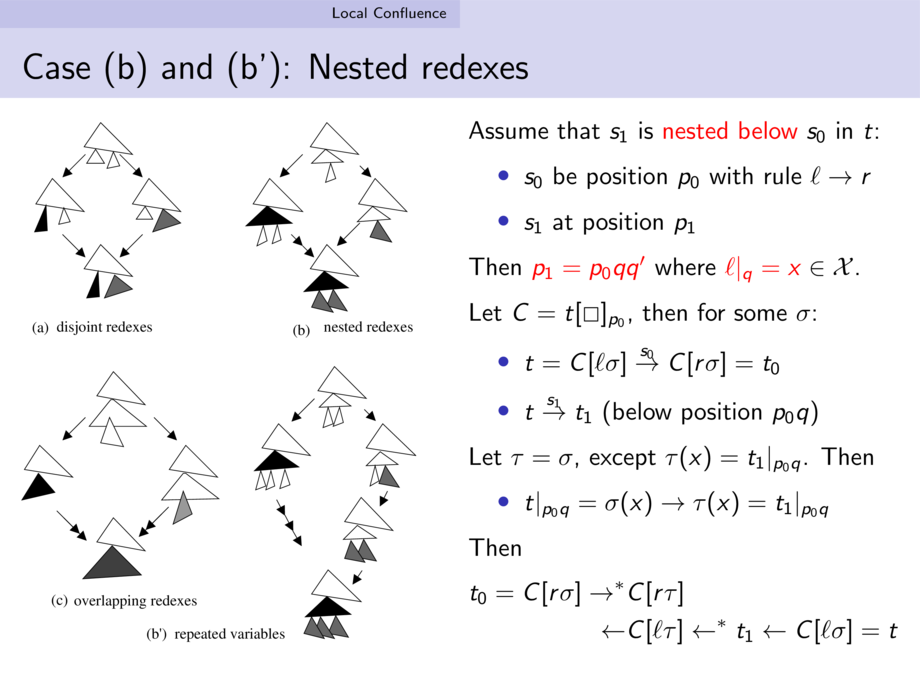
  Assume that $s_1$ is \alert{nested below} $s_0$ in $t$:
  \pause
  \begin{itemize}
    \item $s_0$ be position $p_0$ with rule $\ell \to r$
    \item $s_1$ at position $p_1$
  \end{itemize}
  \pause
  
  Then \alert{$p_1 = p_0 q q'$}  where $\alert{\ell|_q = x} \in \mathcal{X}$.
  \medskip\pause
  
  Let $C = t[\Box]_{p_0}$, then for some $\sigma$:
  \begin{itemize}
    \item $t = C[\ell \sigma] \stackrel{s_0}{\to} C[r\sigma] = t_0$
  \pause
    \item $t \stackrel{s_1}{\to} t_1$ (below position $p_0q$)
  \end{itemize}
  \pause
  
  Let $\tau = \sigma$, except $\tau(x) = t_1|_{p_0q}$. Then
  \begin{itemize}
    \item $t|_{p_0q} = \sigma(x) \to \tau(x) = t_1|_{p_0q}$
  \end{itemize}
  \pause  
  
  Then\vspace{-1ex}
  \begin{align*}
    t_0 = C[r\sigma] \to^* &C[r\tau]\\
    \leftarrow &C[\ell\tau] \leftarrow^* t_1 \leftarrow C[\ell\sigma] = t
  \end{align*}
  \medskip
  \end{minipage}
\end{frame}