


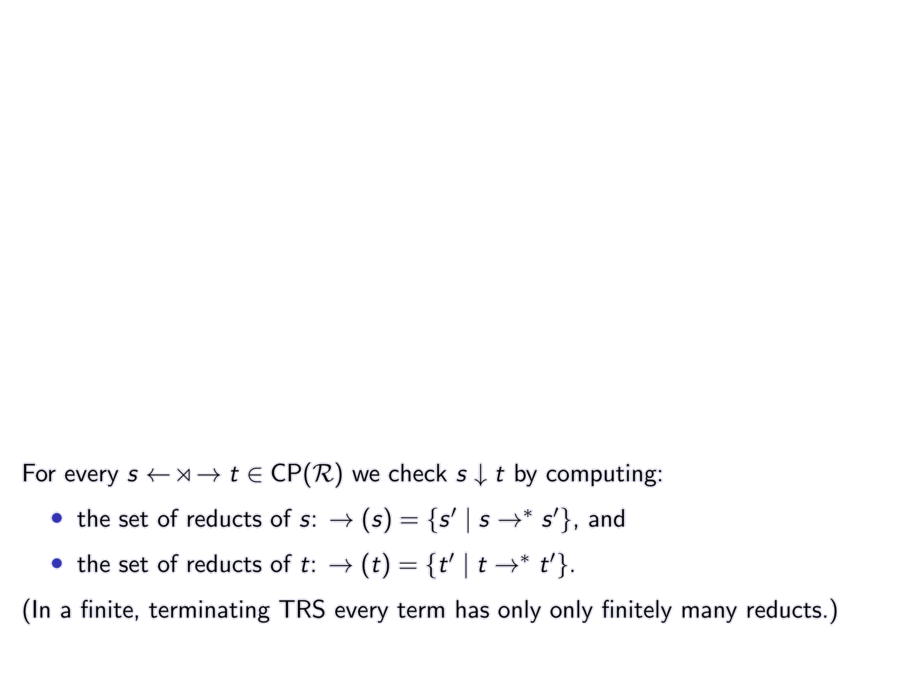






























































































8/145
\begin{frame}[t]
\frametitle{Local Confluence}
\begin{block}{Critical Pair Lemma}
\smallskip
A TRS is locally confluent (WCR) \quad$\iff$\quad all critical pairs are convergent.
\end{block}
\medskip\pause
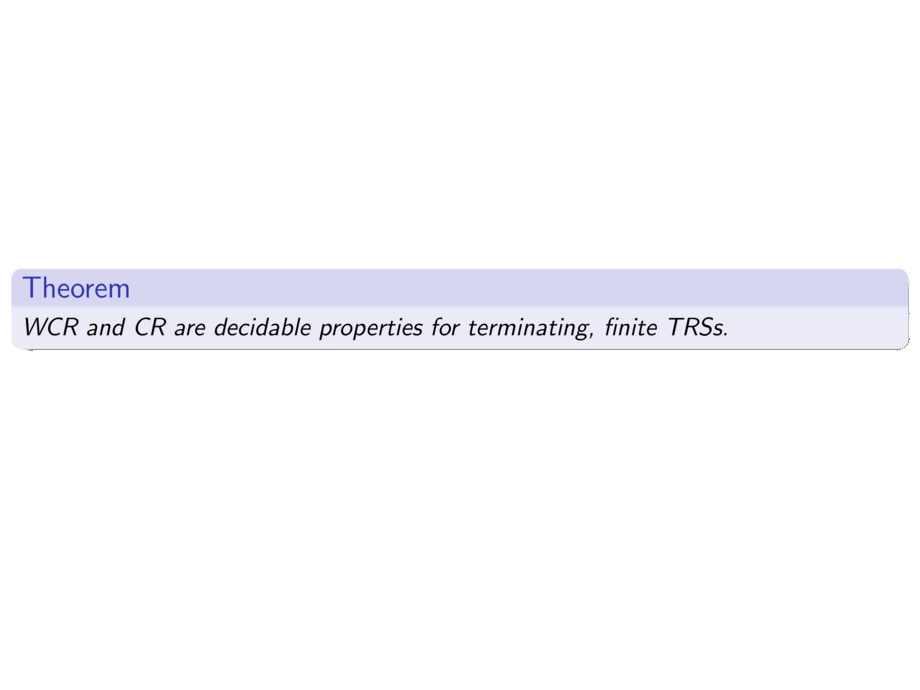
\begin{theorem}
WCR and CR are decidable properties for terminating, finite TRSs.
\end{theorem}
\pause
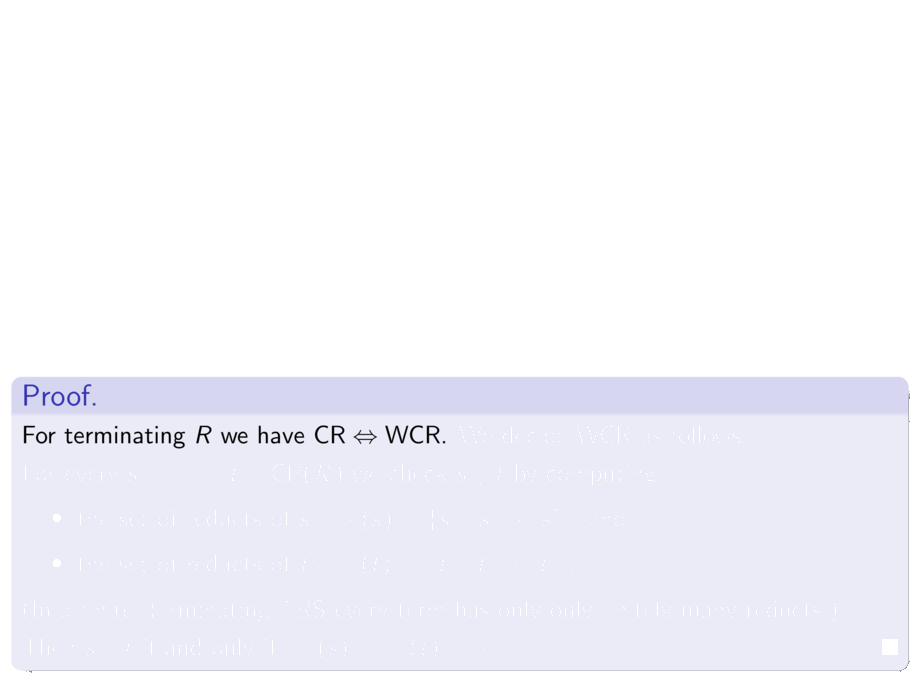
\begin{proof}
For terminating $R$ we have $\text{CR} \Leftrightarrow \text{WCR}$.
\pause
We decide WCR as follows:
\pause
\smallskip
For every $s \cp t \in \CP(\atrs)$ we check $s \join t$ by computing:
\begin{itemize}
\item the set of reducts of $s$: $\to(s) = \{s' \mid s\to^* s'\}$, and
\item the set of reducts of $t$: $\to(t) = \{t' \mid t\to^* t'\}$.
\end{itemize}
(In a finite, terminating TRS every term has only only finitely many reducts.)
\pause\smallskip
Then $s \join t$ if and only if ${\to(s)} \cap {\to(t)} \ne \emptyset$.
\end{proof}
\end{frame}

