


































































































121/205
\begin{frame}
\small
\begin{block}{Invariants}
\smallskip
\begin{enumerate}[<+->]
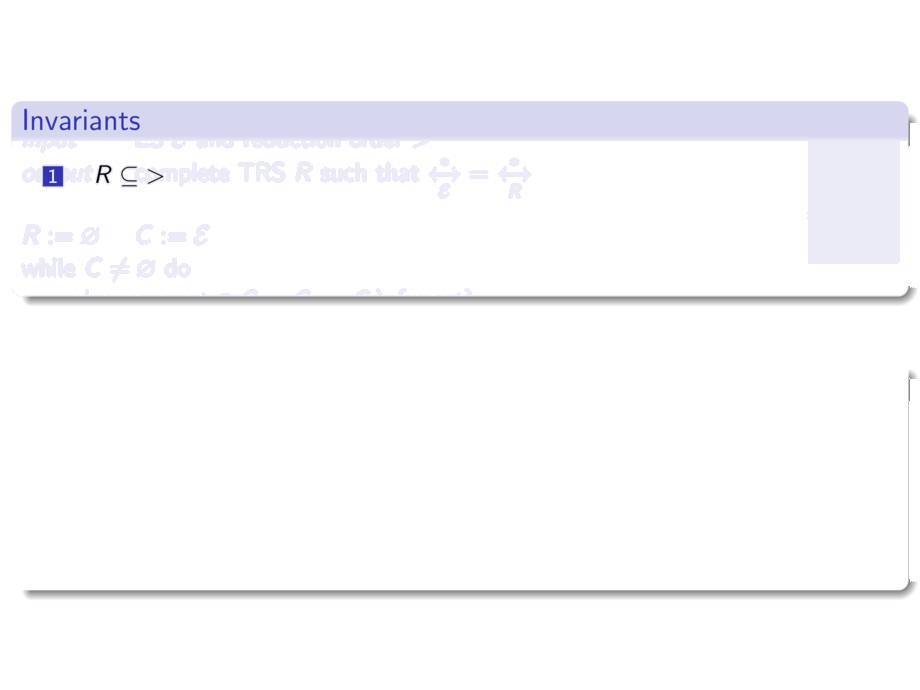
\item~
$\RR \subseteq {>}$
\item~
\smash{$\xleftrightarrow[\EE]{*} ~=~ \xleftrightarrow[\RR \cup C]{*}$}
\item~
equations in $\CP(\RR) \setminus C$ are convergent with respect to $\RR$
\smallskip
\end{enumerate}
\end{block}
\bigskip
\begin{block}<4->{Three Possibilities}
\smallskip
Knuth-Bendix completion procedure may
\begin{enumerate}
\item~
terminate without failure
\onslide<5->
\quad$\Longrightarrow$\quad
$\RR$ is complete and
\smash{$\xleftrightarrow[\EE]{*} ~=~ \xleftrightarrow[\RR]{*}$}
\item<6->~
terminate with failure
\item<7->~
not terminate \qquad \onslide<7->{(\alert{divergence})}
\smallskip
\end{enumerate}
\end{block}
\end{frame}

