


































































































43/205
\begin{frame}
\small
\begin{example}[Group Theory]
\smallskip
\begin{tabular}{l@{\qquad}lc}
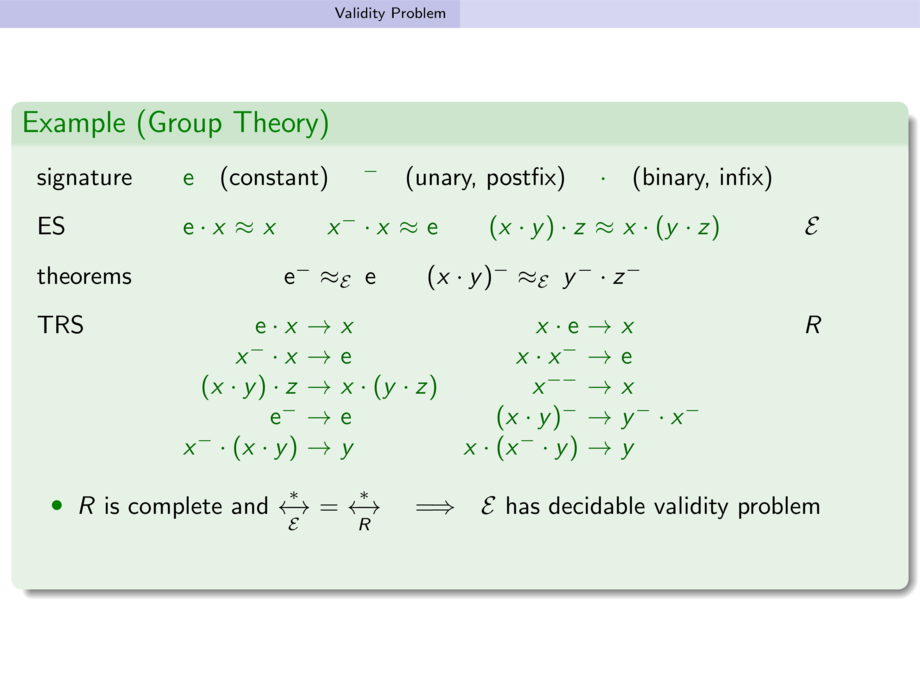
signature &
$\mG{e}$ ~ (constant) \quad \GREEN{${}^-$} ~ (unary, postfix)
\quad \GREEN{$\cdot$} ~ (binary, infix) \\
\\[-1ex]
ES &
\GREEN{$\begin{array}[t]{@{}r@{~}c@{~}l@{\qquad}r@{~}c@{~}l@{\qquad}%
r@{~}c@{~}l@{}}
\m{e} \cdot x &\approx& x &
x^- \cdot x &\approx& \m{e} &
(x \cdot y) \cdot z &\approx& x \cdot (y \cdot z)
\end{array}$} & $\EE$ \\
\\[-1ex]
theorems &
$\begin{array}[t]{@{\qquad\qquad}r@{~}c@{~}l@{\qquad}%
r@{~}c@{~}l@{}}
\m{e}^-
&\makebox[5mm]{$\!\alert<3>{\alt<3->{\downarrow_\RR}{\approx_\EE}}$}&
\m{e} &
(x \cdot y)^-
&\makebox[5mm]{$\!\alert<3>{\alt<3->{\downarrow_\RR}{\approx_\EE}}$}&
y^- \cdot z^-
\end{array}$ \\
\\[-1ex]
TRS &
\GREEN{$\begin{array}[t]{@{}r@{~}c@{~}l@{\quad}r@{~}c@{~}l@{}}
\m{e} \cdot x &\to& x &
x \cdot \m{e} &\to& x
\\
x^- \cdot x &\to& \m{e} &
x \cdot x^- &\to& \m{e}
\\
(x \cdot y) \cdot z &\to& x \cdot (y \cdot z) &
x^{- -} &\to& x
\\
\m{e}^- &\to& \m{e}
& (x \cdot y)^- &\to& y^- \cdot x^-
\\
x^- \cdot (x \cdot y) &\to& y &
x \cdot (x^- \cdot y) &\to& y
\end{array}$} & $\RR$
\end{tabular}
\smallskip
\begin{itemize}
\item<2->
$\RR$ is complete and
$\xleftrightarrow[\EE]{*} ~=~ \xleftrightarrow[\RR]{*}$
\quad$\Longrightarrow$\quad
$\EE$ has decidable validity problem
\item<4->
\makebox[8.6cm][l]{How to compute $\RR$ ?}
\onslide<5->{\alert{completion}}
% (lectures 5 \& 6)}
% \item<6->
% \makebox[5cm][l]{how to prove termination of $\RR$ ?}
% \onslide<7->{\makebox[25mm][l]{\alert{LPO} or \alert{KBO}}
% (lectures 4 \& 7)}
\smallskip
\end{itemize}
\end{example}
\end{frame}

