


































































































60/73
\begin{frame}
\small
\begin{theorem}
\begin{itemize}[<+->]
\item
there are no infinite derivations
\[
\makebox[6cm][l]{$s \approx t
\Rightarrow_{\sigma_1} E_1
\Rightarrow_{\sigma_2} E_2
\Rightarrow_{\sigma_3} \cdots$}
\]
\item
if $s$ and $t$ are unifiable then for every maximal derivation
\[
\makebox[6cm][l]{$s \approx t
\Rightarrow_{\alert<4>{\sigma_1}} E_1
\Rightarrow_{\alert<4>{\sigma_2}} E_2
\Rightarrow_{\alert<4>{\sigma_3}} \cdots
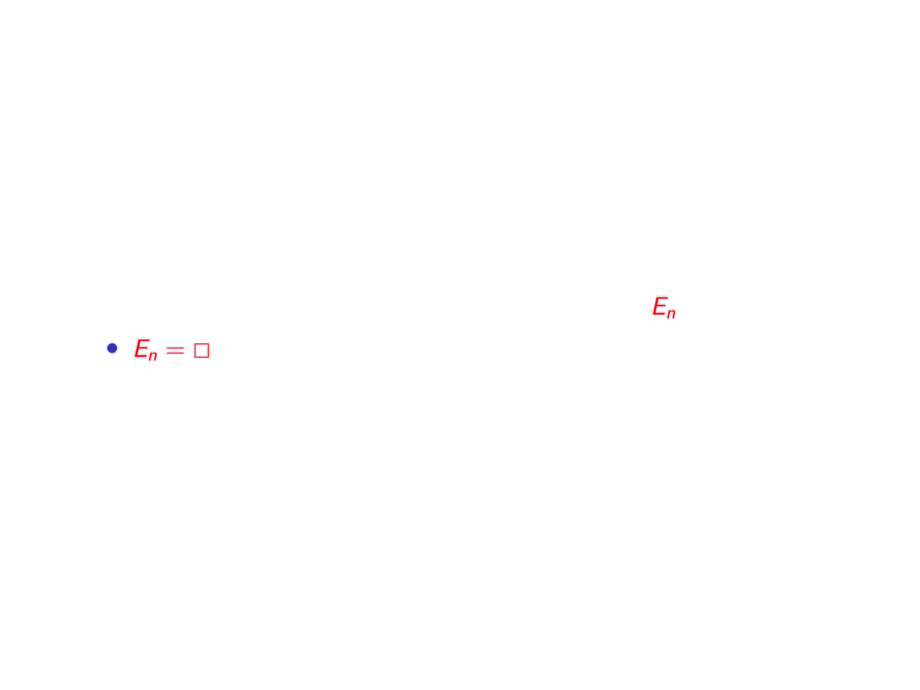
\Rightarrow_{\alert<4>{\sigma_n}} \alert<3>{E_n}$}
\]
\vspace{-5ex}
\begin{itemize}
\item
$\alert<3>{E_n = \Box}$
\medskip
\item<4->
$\alert<4>{\sigma_1\sigma_2\sigma_3 \cdots \sigma_n}$ is mgu of $s$ and $t$
\smallskip
\end{itemize}
\end{itemize}
\end{theorem}
\bigskip
\begin{block}<5->{Optional Failure Rules}
\smallskip
\[
\frac{E_1,\:f(\seq{s}) \approx g(\seq[m]{t}),\:E_2}{\bot}
\qquad
\underset{\raisebox{-1ex}{\small if $x \ne t$ and $x \in \Var(t)$}}{
\frac{E_1,\:x \approx t,\:E_2}{\bot}
\quad
\frac{E_1,\:t \approx x,\:E_2}{\bot}
}
\]
\end{block}
\end{frame}

