\begin{frame}[t]
  \frametitle{Dependency Pairs, Introduction}
  
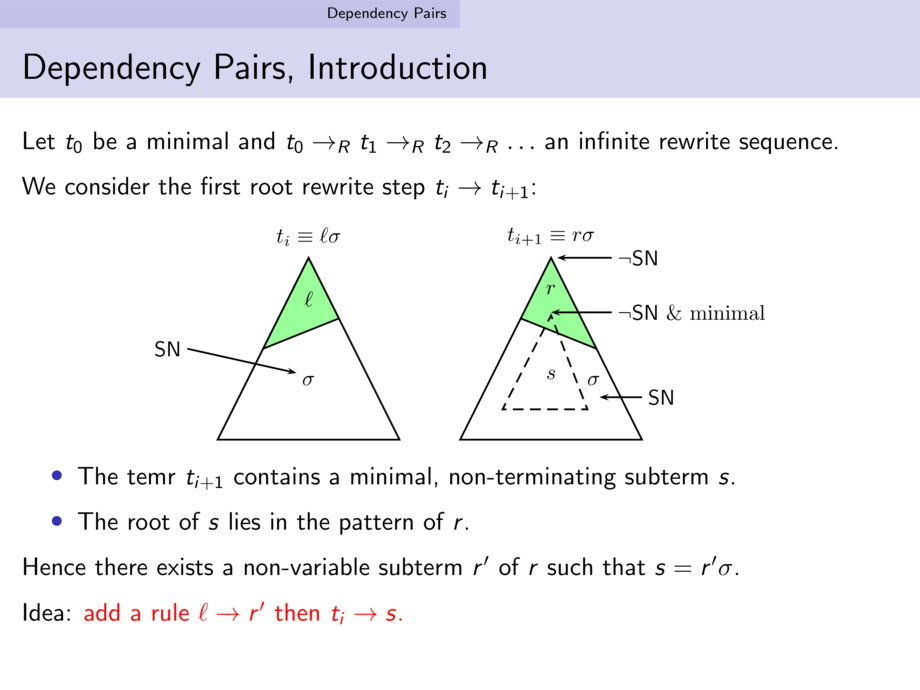
  Let $t_0$ be a minimal and $t_0 \to_R t_1 \to_R t_2 \to_R \ldots$ an infinite rewrite sequence.
  \medskip
  
  We consider the first root rewrite step $t_i \to t_{i+1}$:
  \pause
  
  \only<2->{
  \begin{center}
    \includegraphics[width=.7\textwidth]{../graphics/pstricks/dp_1}
  \end{center}
  \vspace{-1em}
  }
  
  \begin{itemize}
  \pause
   \item The term $t_{i+1}$ contains a minimal, non-terminating subterm $s$.
  \pause
   \item The root of $s$ lies in the pattern of $r$.
  \end{itemize}
  \pause
  Hence there exists a non-variable subterm $r'$ of $r$ such that $s = r' \sigma$.
  \pause\medskip
  
  Idea: \alert{add a rule $\ell \to r'$ then $t_i \to s$.}
\end{frame}