

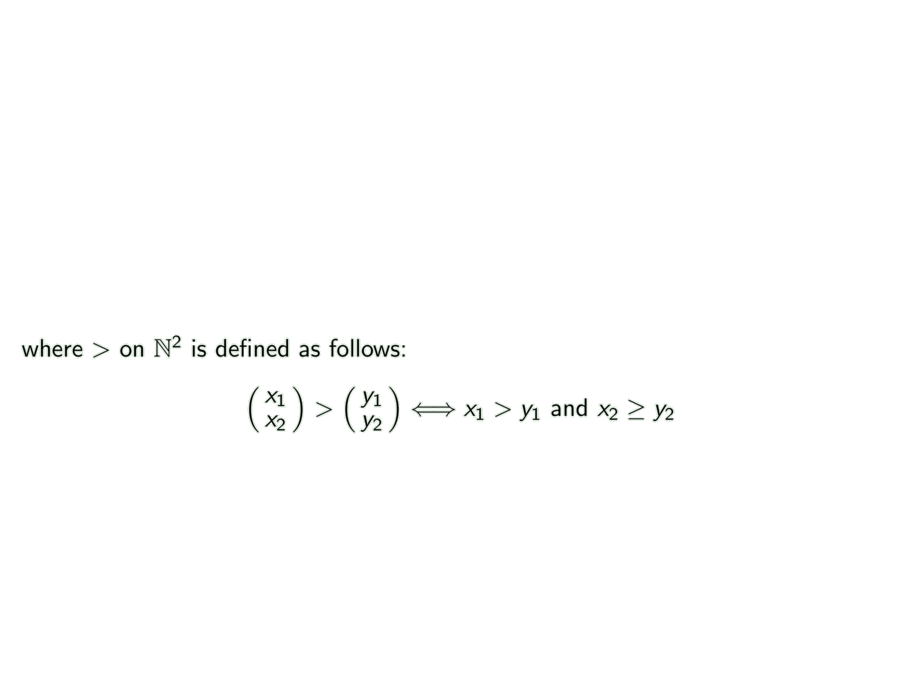

































































































183/365
\begin{frame}
\frametitle{A non-simply terminating TRS: $f(f(x)) \to f(g(f(x)))$}
\begin{example}[$S = \{f(f(x)) \to f(g(f(x)))\}$]
We choose the $\Sigma$-algebra $(\nat^2,\interpret{\cdot})$ with:
\begin{align*}
{\rm [f]}(\vec{x}) &=
\left(\begin{array}{cc}
\emph{1} & 1\\
0 & 0\\
\end{array} \right) \cdot \vec{x}
+
\left(\begin{array}{c}
0\\
1\\
\end{array} \right)
&
{\rm [g]}(\vec{x}) &=
\left(\begin{array}{cc}
\emph{1} & 0\\
0 & 0\\
\end{array} \right) \cdot \vec{x}
+
\left(\begin{array}{c}
0\\
0\\
\end{array} \right)
\end{align*}
\vspace{-0.5em}
\pause
where $>$ on $\nat^2$ is defined as follows:
\begin{align*}
\left(\begin{array}{c}
x_1\\
x_2\\
\end{array} \right)
>
\left(\begin{array}{c}
y_1\\
y_2\\
\end{array} \right)
\Longleftrightarrow
x_1 > y_1 \text{ and } x_2 \ge y_2
\end{align*}
\vspace{-0.5em}
\pause
Let $\alpha{:}\ {\cal X} \to A$ be arbitrary; write $\vec{x} = \alpha(x)$.
We obtain
\begin{align*}
[f(f(x))] =
\left(\begin{array}{cc}
1 & 1\\
0 & 0\\
\end{array} \right) \cdot \vec{x}
+
\left(\begin{array}{c}
\emph{1}\\
1\\
\end{array} \right)
&>
\left(\begin{array}{cc}
1 & 1\\
0 & 0\\
\end{array} \right) \cdot \vec{x}
+
\left(\begin{array}{c}
\emph{0}\\
1\\
\end{array} \right)
= [f(g(f(x)))]
\end{align*}
\vspace{-0.5em}
\pause
Hence $S$ is terminating.
\end{example}
\end{frame}

