







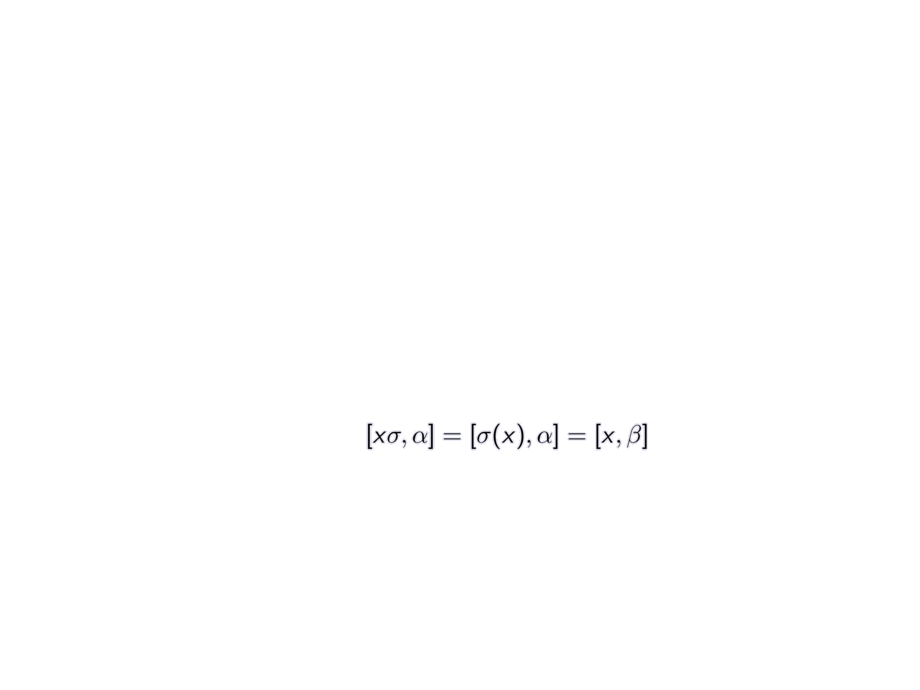



























































































80/365
\begin{frame}
\begin{lemma}
Let $\AA$ well-founded monotone $\Sigma$-algebra.
Then $>_\AA$ is closed under substitutions.
\end{lemma}
\pause
\begin{proof}
Let $s,t \in \TTlong$ such that $t >_\AA s$.\pause\smallskip
Let $\sigma$ be a substitution. We show $t\sigma >_\AA s\sigma$.\pause\smallskip
That is: $[t\sigma,\alpha] > [s\sigma,\alpha]$ for every $\alpha : \VV \to A$.\pause\smallskip
Define $\beta : \VV \to A$ by $\beta(x) = \interpret{\sigma(x),\alpha}$.
\pause
Claim: $\interpret{u\sigma,\alpha} = \interpret{u,\beta}$ for all $u$.
\begin{itemize}
\item<7->
\pause
Proof of the claim by induction over the term structure of $u$:
\vspace{-.6em}
\begin{align*}
\onslide<8-> \interpret{x\sigma,\alpha} &\onslide<8->= \interpret{\sigma(x),\alpha} = \interpret{x,\beta}\\
\onslide<9->
\interpret{f(t_1,\ldots,t_n)\sigma,\alpha}
&\onslide<10-> = \interpret{f}(\interpret{t_1\sigma,\alpha},\ldots,\interpret{t_n\sigma,\alpha})\\
&\onslide<11-> \stackrel{\text{IH}}{=} \interpret{f}(\interpret{t_1,\beta},\ldots,\interpret{t_n,\beta})\\
&\onslide<12-> = \interpret{f(t_1,\ldots,t_n),\beta}
\end{align*}
\end{itemize}
\vspace{-1.5em}
\onslide<13->
Hence $[t\sigma,\alpha] = [t,\beta] > [s,\beta] = [s\sigma,\alpha]$.
\end{proof}
\end{frame}

