





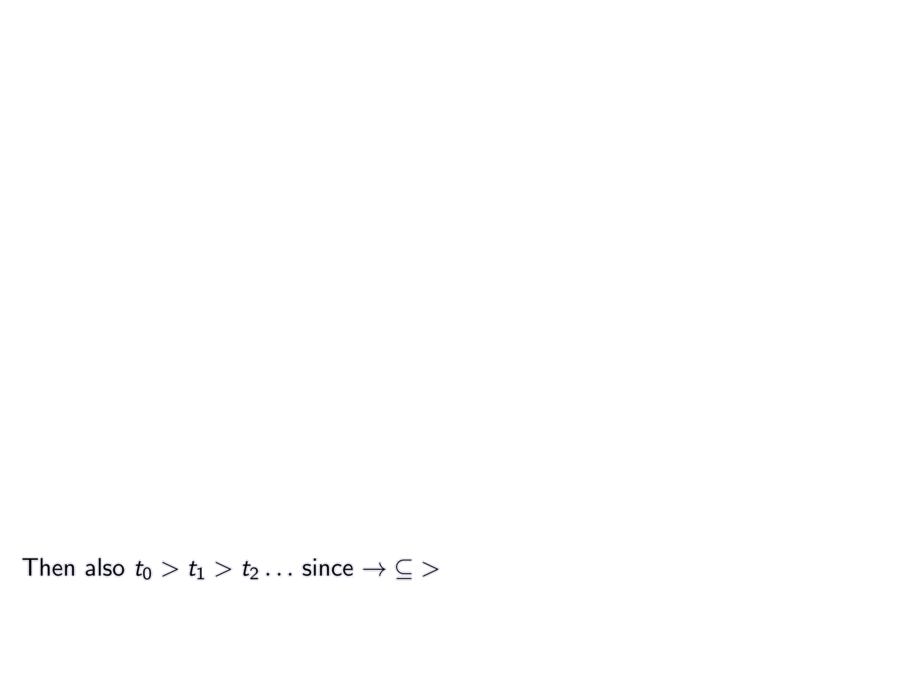





























































































54/365
\begin{frame}
\begin{theorem}
\smallskip
TRS $\RR$ is terminating
\quad$\iff$\quad
$\RR \subseteq {>}$ for reduction order $>$
\end{theorem}
\begin{proof}[Proof $\Leftarrow$]
\pause
Let $>$ be reduction order such that ${R} \subseteq {>}$.\pause\medskip
Recall that $\to$ is the smallest relation $S$ such that:
\begin{itemize}
\item ${R} \subseteq {S}$,
\item $S$ is closed under contexts, and
\item $S$ is closed under substitutions.
\end{itemize}
\pause
Then ${\to} \subseteq {>}$ since ${>}$ has these properties.
\medskip
\pause
Assume there exists an infinite rewrite sequence:
$t_0 \to t_1 \to t_2 \ldots$
\medskip
\pause
Then also
$t_0 > t_1 > t_2 \ldots$ since ${\to} \subseteq {>}$
\medskip
\pause
However, this contradicts well-foundedness of $>$.
\end{proof}
\end{frame}

