


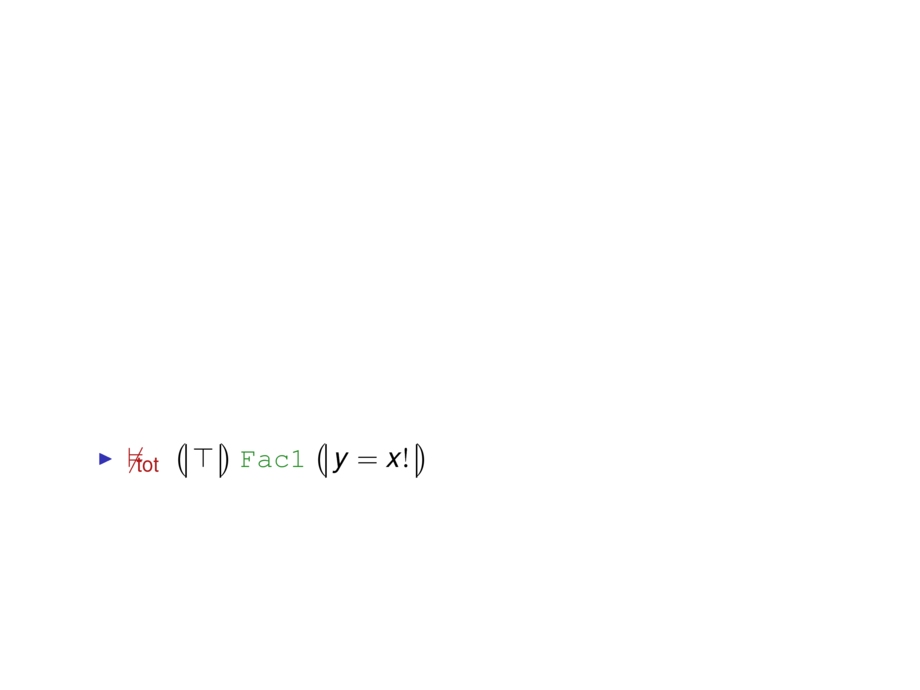
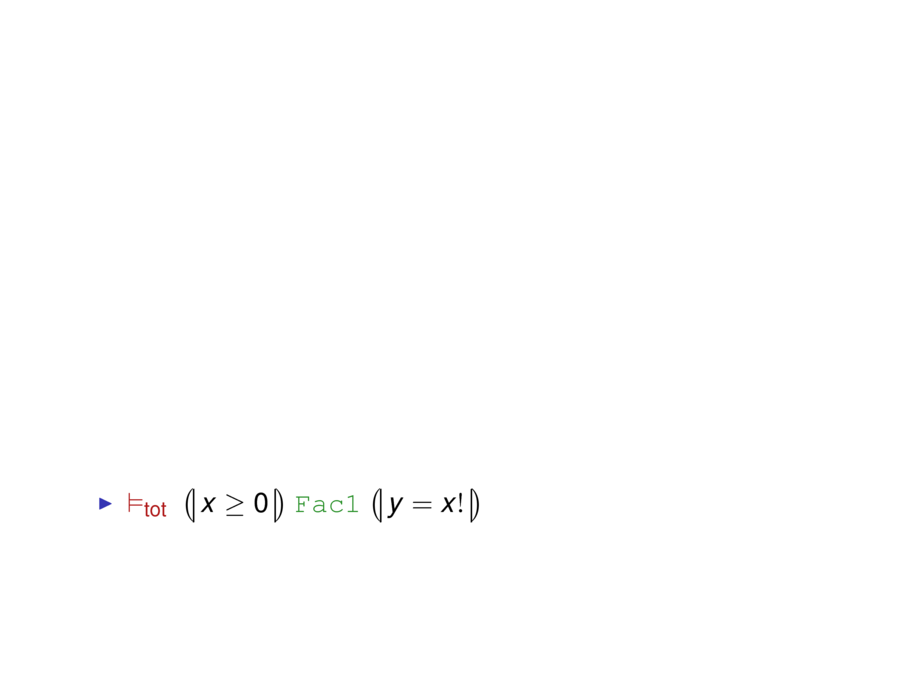

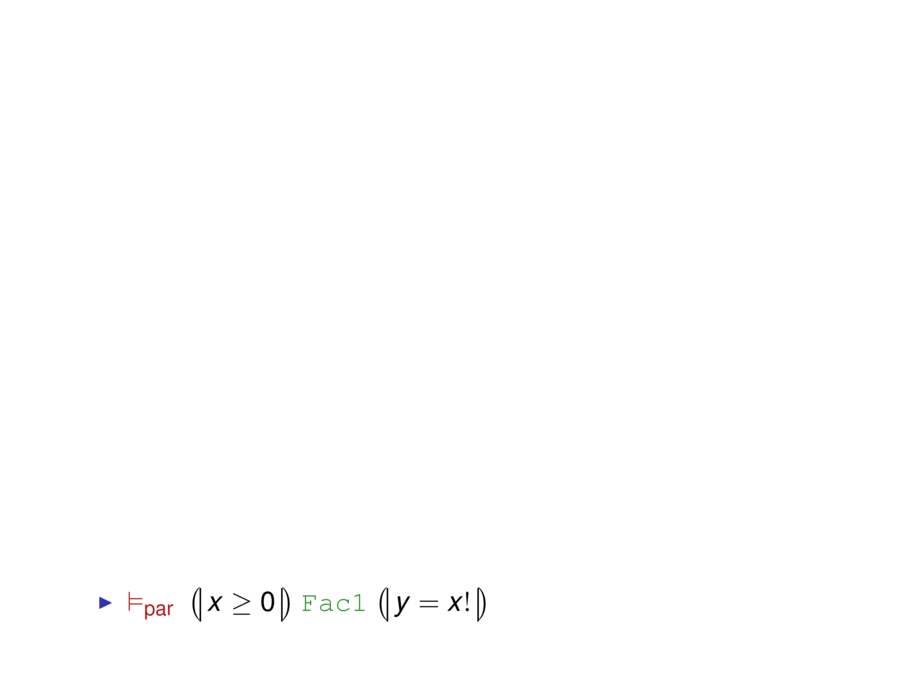





























































































113/191
\begin{frame}[fragile,t]{Partial and Total Correctness}
\vspace*{-1ex}
\begin{exampleblock}{\forestgreen{\tt Fac1}}
\vspace*{-1.25ex}
\begin{lstlisting}
y = 1;
z = 0;
while (z != x) {
z = z + 1;
y = y * z;
}
\end{lstlisting}
\vspace*{-1.25ex}
\end{exampleblock}
Does not terminate for $x < 0\,$!
\pause\medskip
Therefore for total correctness, we expect to be able to prove:
\begin{itemize}
\pause
\item $\satisfiesnottot \hoaretriple{\formula{\true}}{\forestgreen{\texttt{Fac1}}}{\formula{y = \fac{x}}}$
\pause
\item $\satisfiestot \hoaretriple{\formula{x \ge 0}}{\forestgreen{\texttt{Fac1}}}{\formula{y = \fac{x}}}$
\end{itemize}
\pause\medskip
And for partial correctness we expect:
\begin{itemize}
\pause
\item $\satisfiespar \hoaretriple{\formula{x \ge 0}}{\forestgreen{\texttt{Fac1}}}{\formula{y = \fac{x}}}$
\pause
\item $\satisfiespar \hoaretriple{\formula{\true}}{\forestgreen{\texttt{Fac1}}}{\formula{y = \fac{x}}}$
\end{itemize}
\end{frame}

