\begin{frame}
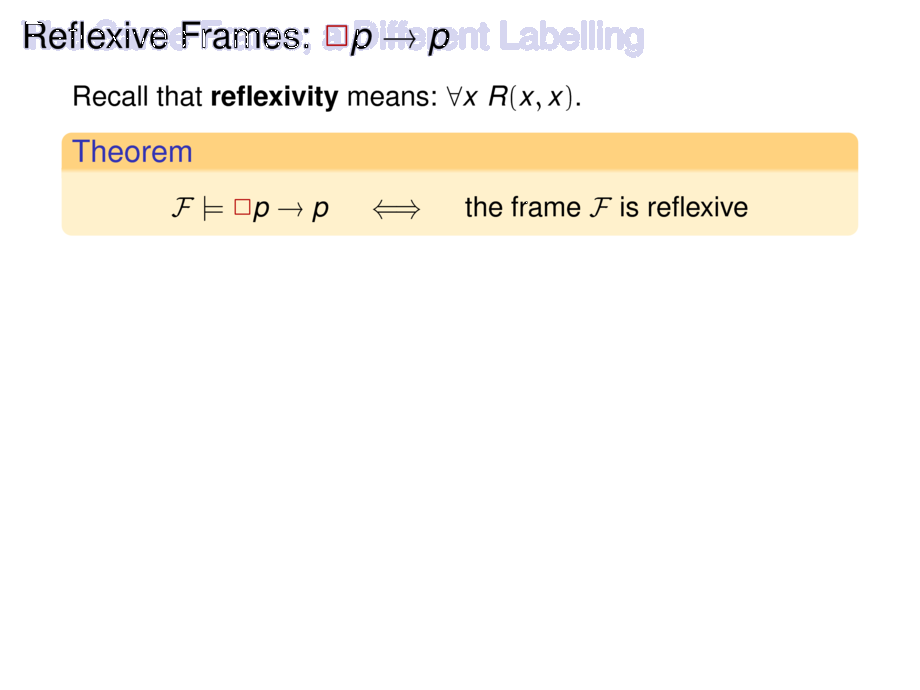
  \frametitle{Reflexive Frames: $\all p \to p$}

  Recall that \emph{reflexivity} means: $\myall{x}{R(x,x)}$.
  \smallskip
  
  \begin{goal}{Theorem}
    \begin{malign}
      \F \models \all p \to p \quad\iff\quad \text{the frame $\F$ is reflexive}
    \end{malign}
  \end{goal}
  \pause\medskip
  
  \alt<-8>{
  \begin{block}{Proof} 
    \begin{itemize}
    \item [$\Leftarrow$]
      Assume that $\F = \pair{W}{R}$ is reflexive. 
      \smallskip\pause

      We show that $\F \models \all p \to p$.
      \smallskip\pause
      
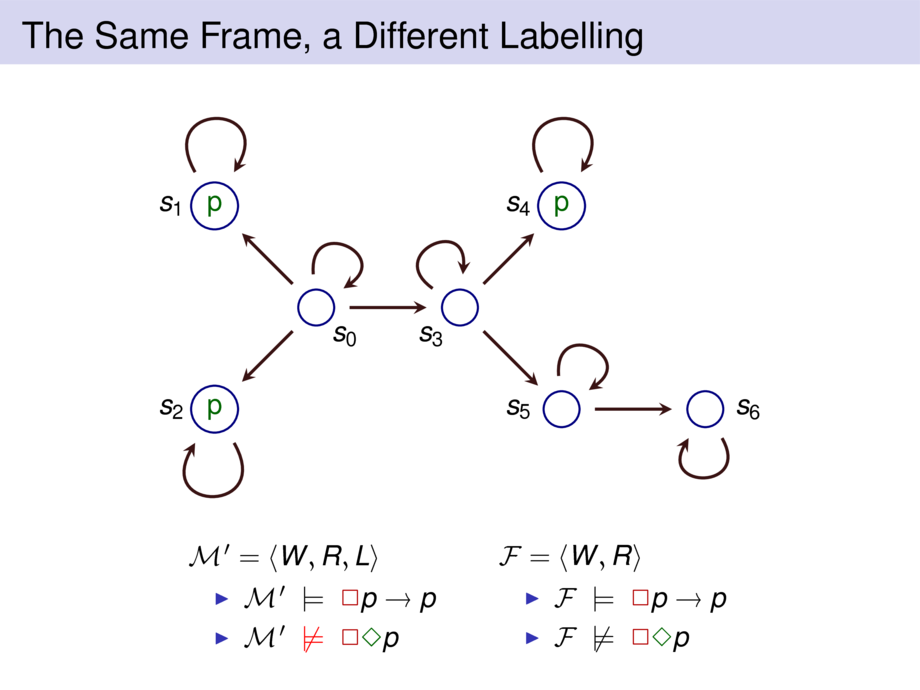
      Let $L$ be an arbitrary labelling and $\M = \langle W,R,L \rangle$.
      \smallskip\pause
      
      We show for every world $x$:\; $\M,x \fc \all p \to p$.
      \smallskip\pause
      
      If \;\;$x \fc \all p$\;\;, then \pause \;\;$x \fc p$\;\; since $R(x,x)$.
      \smallskip\pause
      
      Hence $\M,x \fc \all p \to p$.
    \end{itemize}
  \end{block}
  }{
  \pause[9]
  \begin{block}{Proof} 
    \begin{itemize}
    \item [$\Rightarrow$]
      Assume that $\F \models \all p \to p$.
      \pause
      We show that $\F$ is reflexive. 
      \smallskip\pause
      
      Assume, for a contradiction, $\F$ was not reflexive.
      \smallskip\pause
      
      Then there is a world $a$ with $\neg R(a,a)$.
      \smallskip\pause
            
      Let $\M = \langle W,R,\lab{L} \rangle$ where $\lab{L}$ is given by:\pause
      \begin{talign}
        \lab{L}(a) &= \emptyset  &&&
        \lab{L}(w) &= \{\;p\;\}  \quad \text{for every world $w \neq a$}
      \end{talign}
      \pause
      Then $a \fc \all p$ since $p$ holds in all worlds $\ne a$ \;and\; $\neg R(a,a)$.\\
      \smallskip\pause
       
      But $a \not\fc p$. \pause Thus $a \not\fc \all p \to p$.\\
      \smallskip\pause

      Thus $\F \not\fc \all p \to p$\pause; a contradiction! \pause Hence $\F$ is reflexive. 
    \end{itemize}
  \end{block}
  }
  \vspace{5cm}
  \onslide<19>{}
\end{frame}