
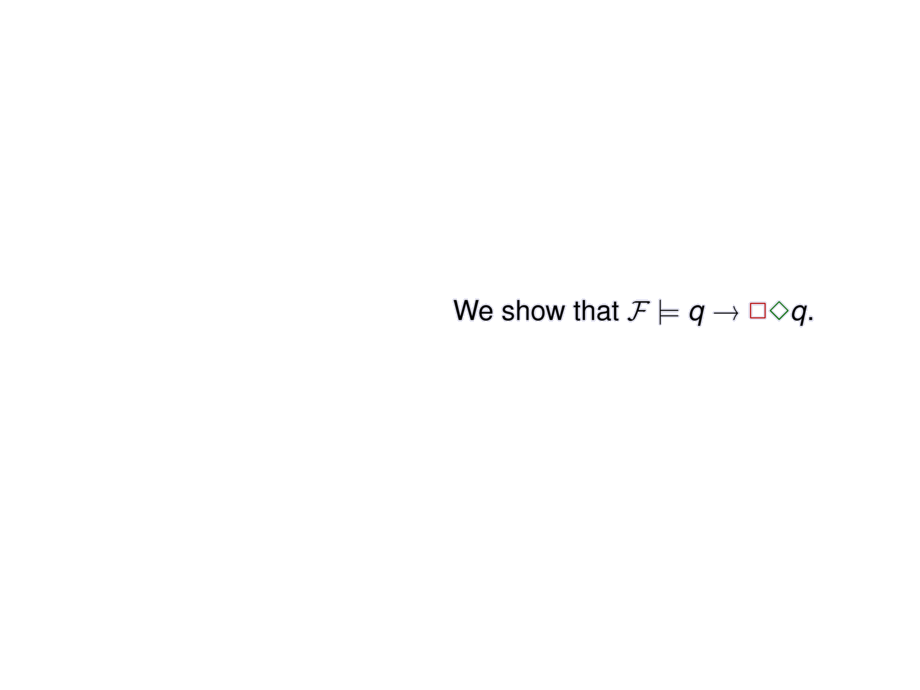
































































































33/122
\begin{frame}
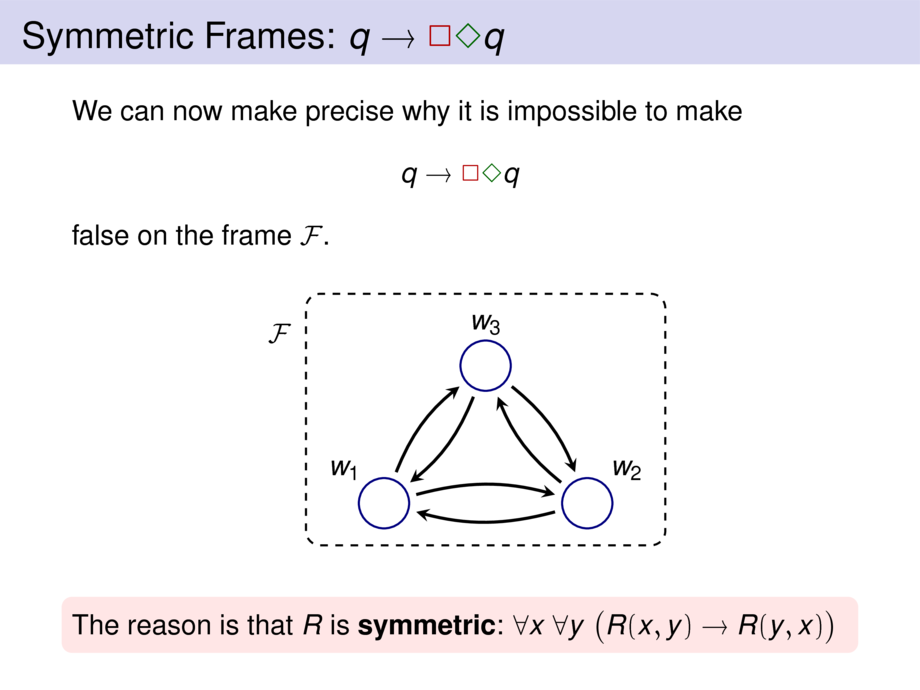
\frametitle{Symmetric Frames: $q \to \all\some q$}
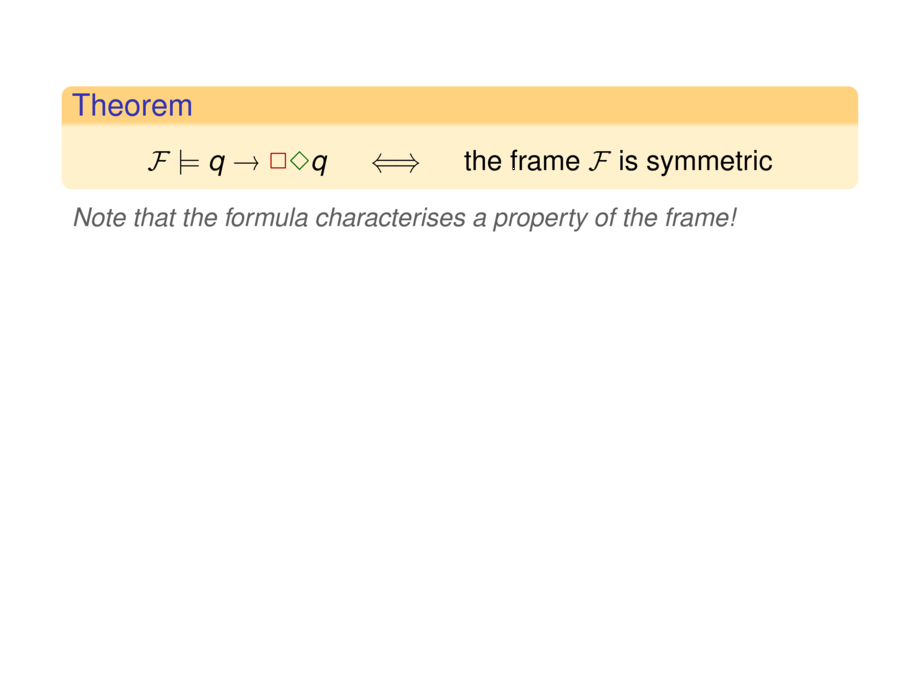
\begin{goal}{Theorem}
\begin{malign}
\F \models q \to \all\some q \quad\iff\quad \text{the frame $\F$ is symmetric}
\end{malign}
\end{goal}
\hint{Note that the formula characterises a property of the frame!}
\pause
\alt<-5>{
\begin{block}{Proof ($\Leftarrow$)}
Let $\F = \pair{W}{R}$ be symmetric. \pause
We show that $\F \models q \to \all\some q$.
\pause\smallskip
That is: $\M \models q \to \all\some q$
for $\M = \langle W,R,L \rangle$ with arbitrary $L$.
\pause\smallskip
Let $x \in W$ be a world. Then (we reason as before)
\begin{itemize}
\item Assume that $q \not\in L(x)$, \\
then $x \fc q \to\all\some q$ \tabto{3.5cm} since $\;x \not\fc q$
\item Assume that $q \in L(x) $, \\
then $x \fc q \to \all\some q$
\tabto{3.5cm} since $\;x \fc \all\some q$
\tabto{3.5cm} since $\;x' \fc \some q$ for all $x'$ with $R(x,x')$
\tabto{3.5cm} since $\;x\fc q$
\end{itemize}
Hence $x \fc q \to \all\some q$.
\end{block}
}{
\pause[6]
\begin{block}{Proof ($\Rightarrow$)}
Let $\F \models q \to \all\some q$. \pause
We show that $\F$ is symmetric.
\pause\smallskip
For a contradiction, assume that $\F$ is not symmetric.
\begin{itemize}
\pause
\item Let $a,b \in W$ with $R(a,b)$ and $\neg R(b,a)$.
\pause
\item Define $\M = \langle W,R,\lab{L} \rangle$ with labelling $\lab{L}$ given by\pause
\begin{malign}
\lab{L}(a) &= \{\;q\;\} &&& \lab{L}(x) = \emptyset \quad\text{for all $x \ne a$}
\end{malign}
\item \pause Then
\begin{itemize}
\pause
\item $a \fc q$ \tabto{2cm}since $q \in \lab{L}(a)$
\pause
\item $b \not\fc \some q$ \tabto{2cm}since $q$ is valid only in $a$ \;and\; $\neg R(b,a)$
\pause
\item $a \not\fc \all\some q$ \tabto{2cm}since $b \not\fc \some q$ \;and\; $R(a,b)$
\end{itemize}
\pause
\item Hence $\F \not\models q \to \all\some q$; a contradiction.
\end{itemize}
\end{block}
}
\bigskip
\onslide<15>{}
\end{frame}

