\begin{frame}
  \frametitle{A \emph{Frame} is a Kripke Model without Labelling}
  
  \begin{goal}{}
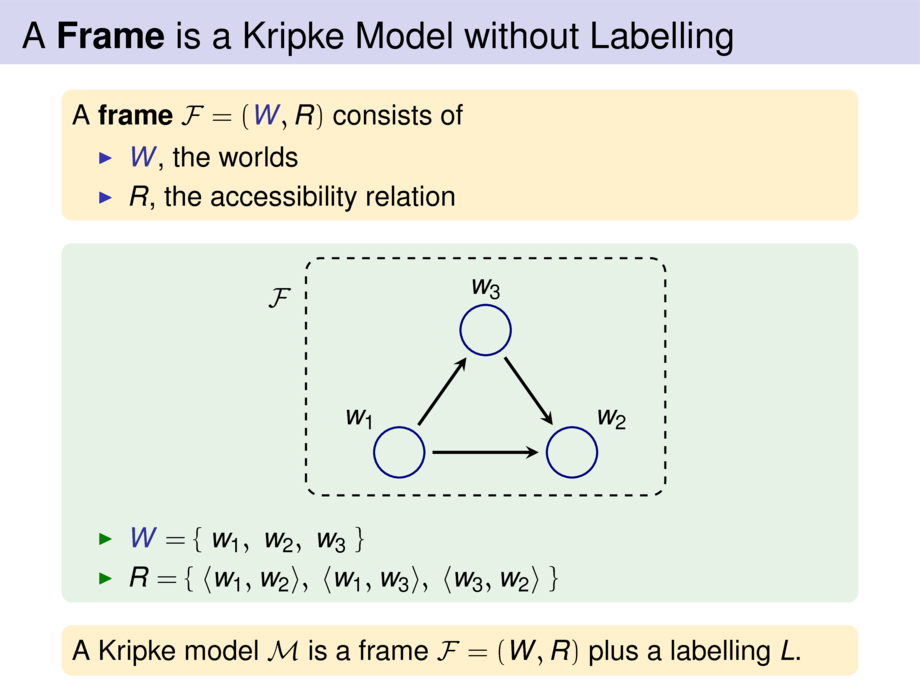
    A \emph{frame} $\mathcal{F} = (\BLUE{W},R)$ consists of
    \begin{itemize}
      \item $\BLUE{W}$, the worlds
      \item $R$, the accessibility relation 
    \end{itemize}
  \end{goal}

  \begin{exampleblock}{}
    \begin{center}
    \begin{tikzpicture}[
        default,
        point/.style={circle, draw=blue, thick, inner sep=3pt, minimum size=7mm},
        node distance=17mm]
  
      \node (3) [point] {};
      \node [ao=3] {$w_3$};
      
      \node (2) [point, below right of=3,yshift=-5mm] {};
      \node [aro=2] {$w_2$};

      \node (1) [point, below left of=3,yshift=-5mm] {};
      \node [alo=1] {$w_1$};

      \begin{scope}[shorten <= 1mm, shorten >= 1mm, very thick,>=stealth]
        \draw [->] (1) to (2);
        \draw [->] (1) to (3);
        \draw [->] (3) to (2);
      \end{scope}

      \draw [rounded corners=2mm, dashed] (-25mm,-23mm) rectangle (25mm,10mm);
      \node at (-25mm,8mm) [anchor=north east,inner sep=2mm] {$\mathcal{F}$};
    \end{tikzpicture}
    \end{center}
    \vspace{-2ex}

    \begin{itemize}  
      \item  $\BLUE{W}= \{\; w_1,\; w_2,\; w_3 \; \}$
      \item  $R = \{ \;\pair{w_1}{w_2},\; \pair{w_1}{w_3},\; \pair{w_3}{w_2}\; \}$
    \end{itemize}    
  \end{exampleblock}
  \pause
  
  \begin{goal}{}
    A Kripke model $\M$ is a frame $\F = (W,R)$ plus a labelling $L$.
  \end{goal} 
\end{frame}