

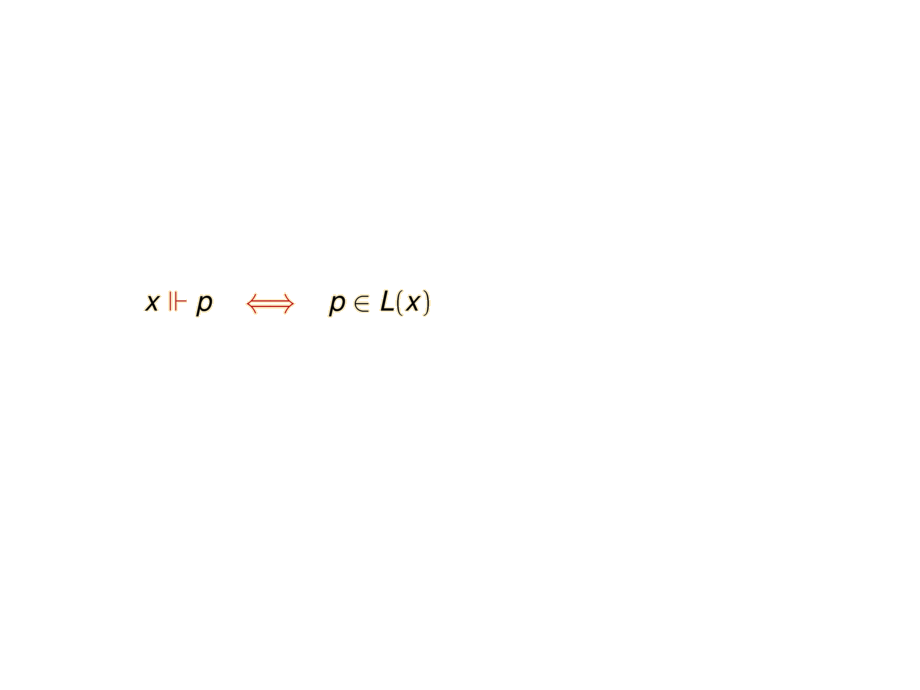
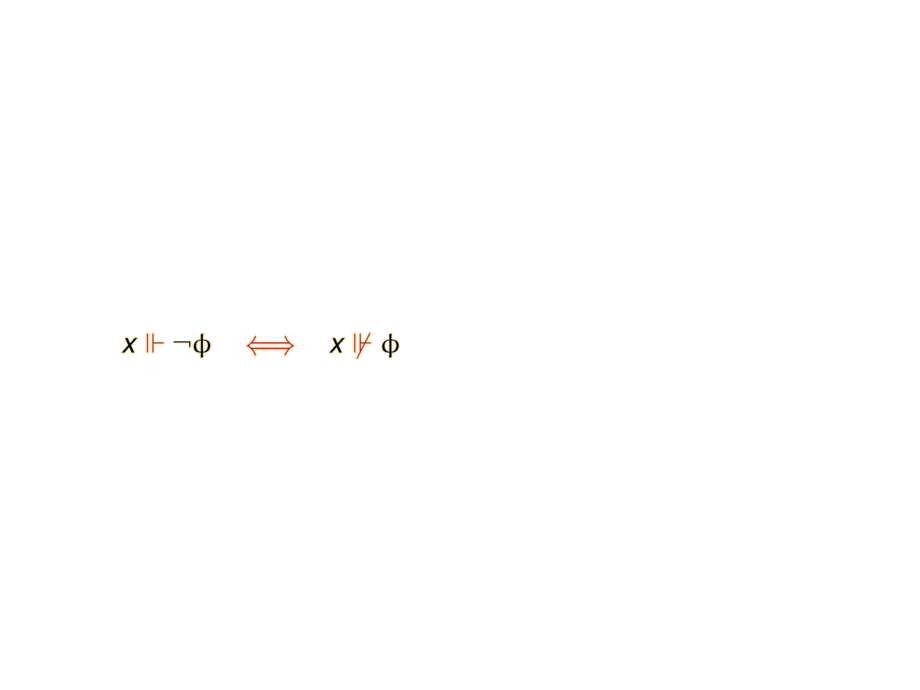
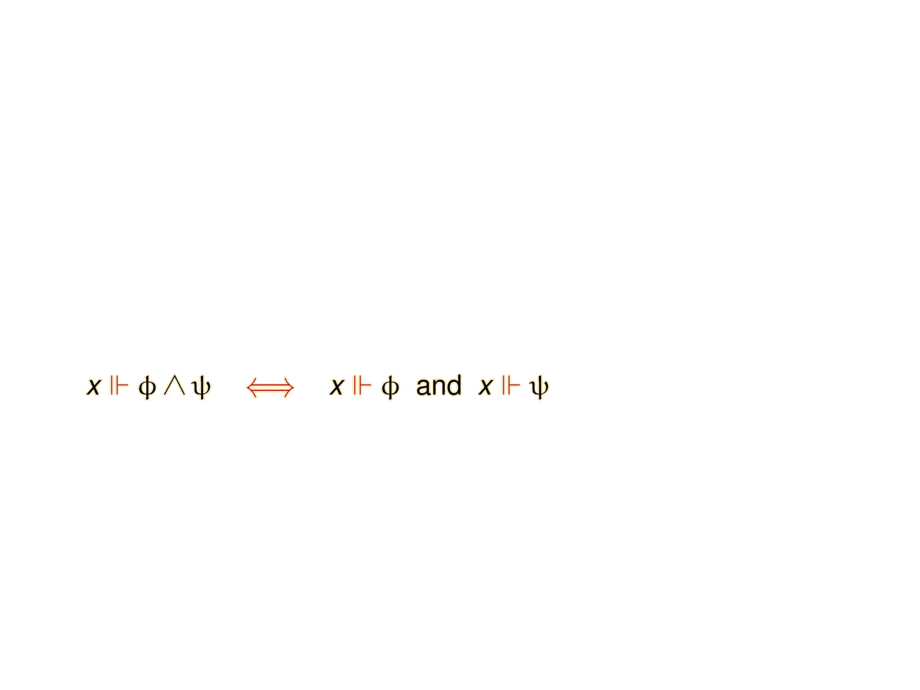
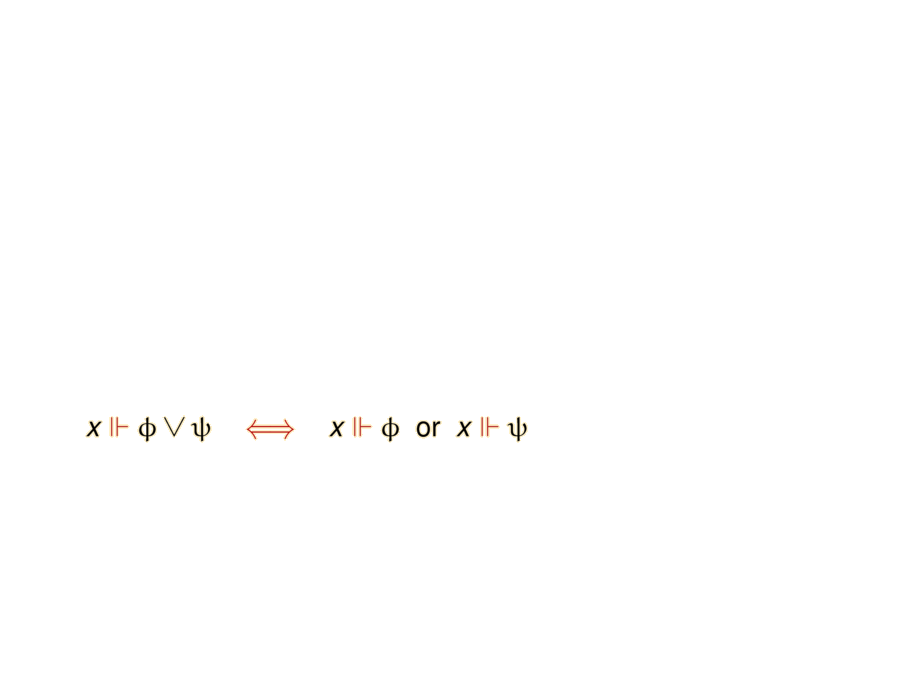
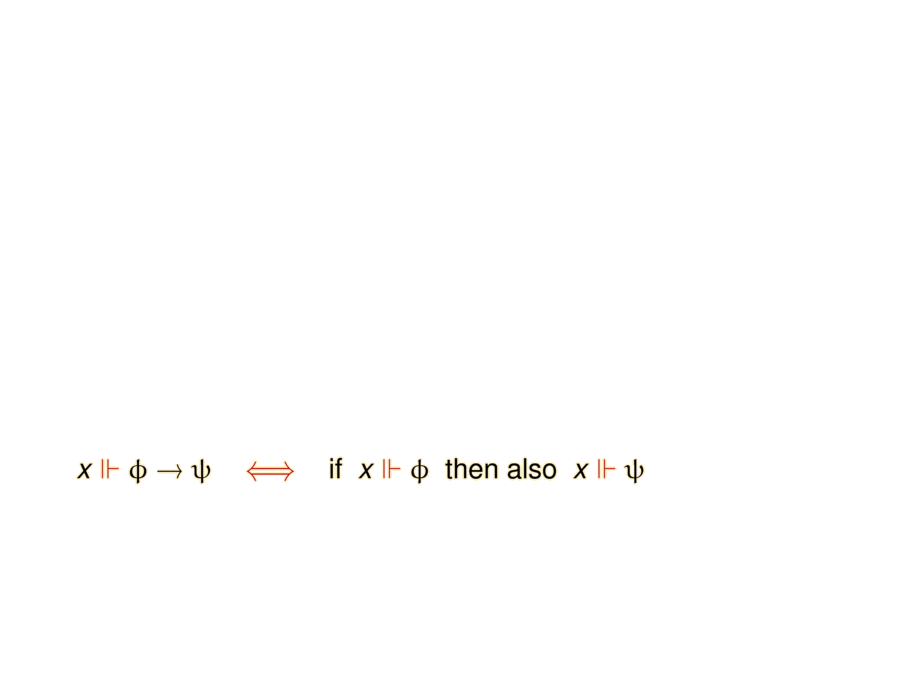
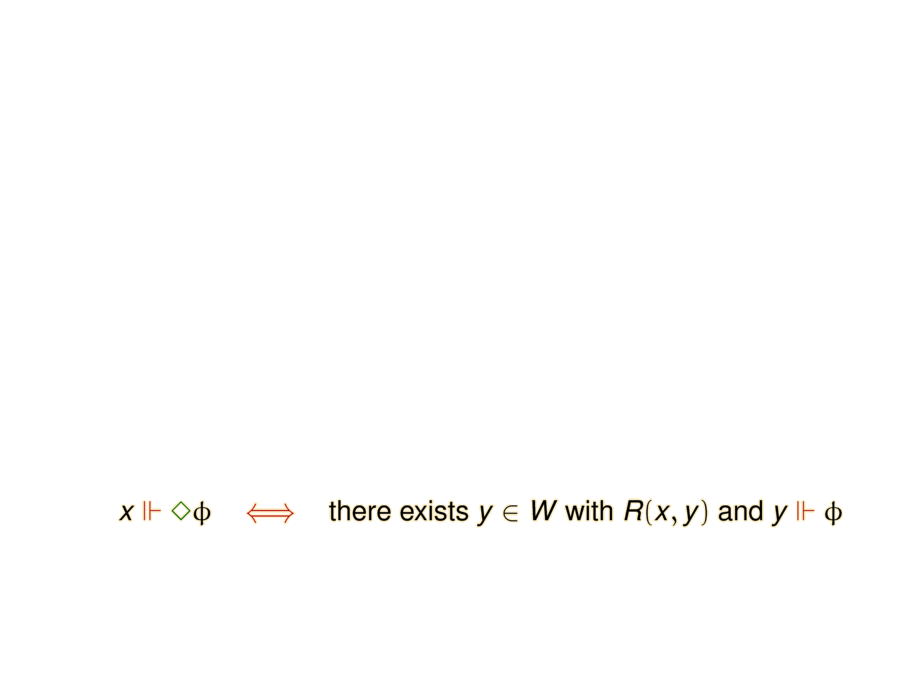



























































































82/158
\begin{frame}
\frametitle{Formal Definition of Truth in Worlds}
In Kripke model $\mathcal{M} = (W, R, L)$ we first define \emph{truth} \aemph{per world}.
\bigskip\pause
\begin{goal}{Definition of $\mathcal{M},x \fc \phi$}
\vspace{-2ex}
\begin{eqnarray*}
x \notfc \bot &&\\
\mpause[1]{ x \fc p & \riff & p\in L(x) } \\
\mpause{ x \fc \neg \phi & \riff & x\notfc \phi } \\
\mpause{ x \fc \phi \wedge \psi & \riff & x \fc \phi \;\;\mbox{and} \;\; x\fc \psi } \\
\mpause{ x \fc \phi \vee \psi & \riff & x \fc \phi \;\;\mbox{or} \;\; x\fc \psi } \\
\mpause{ x \fc \phi \to \psi & \riff & \mbox{if} \;\; x \fc \phi \;\;\mbox{then also} \;\; x\fc \psi } \\
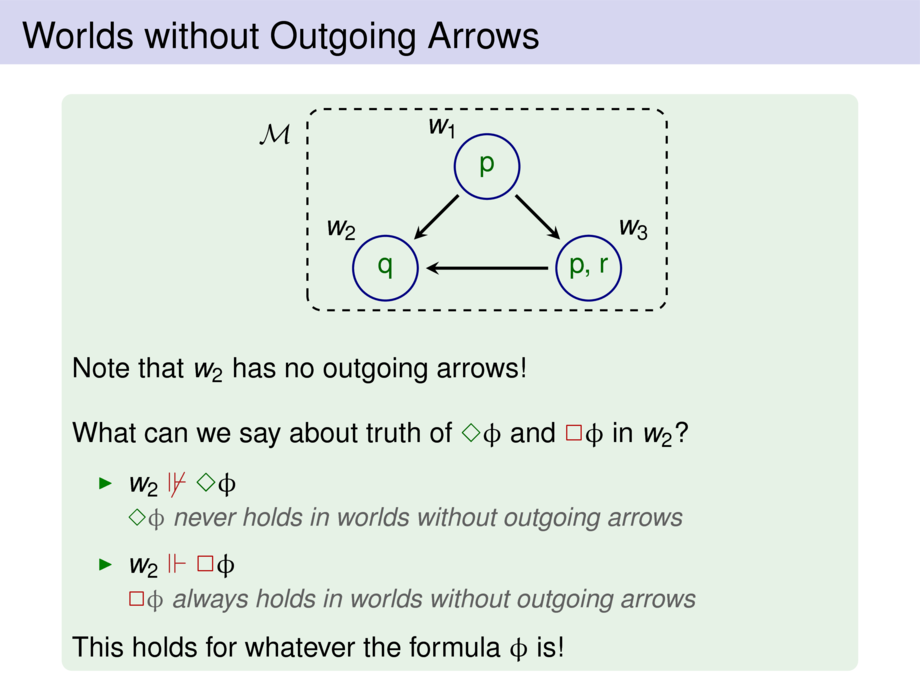
\mpause{ x \fc \some \phi &\riff& \mbox{there exists $y \in W$ with $R(x,y)$ and $y\fc\phi$} } \\
\mpause{ x \fc \all \phi &\riff& \mbox{for all $y\in W$ with $R(x,y) $ holds:\; $y\fc\phi $}}
\end{eqnarray*}
\vspace{-2ex}
\end{goal}
\mpause{
\hint{Note the analogy with the truth definition in predicate logic.}
}
\end{frame}

