






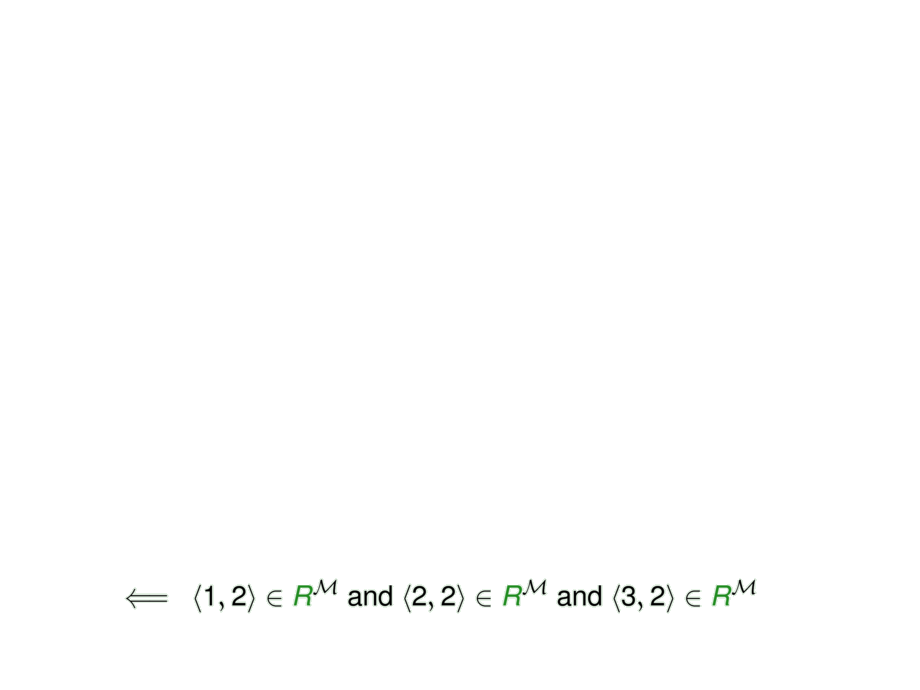



























































































230/270
\begin{frame}{Checking Formula Satisfiability in a Model}
\vspace*{-0.75ex}
\begin{exampleblock}{
\black{$\model{\amodel} \satisfies \formula{\existsst{y}{\forallst{x}{\,\binpred{R}{x}{y}}}}$
\hspace*{1.75ex} for model \hspace*{1ex}
\parbox[c]{0.3\textwidth}{
\begin{tikzpicture}[node distance=15mm,scale=0.9,
dot/.style={minimum size=4mm, circle, draw=none, fill=black, inner sep=0, outer sep=1mm,text=white,scale=0.9}]
\node [dot] (1) {1};
\node [dot,below right of=1] (2) {2};
\node [dot,above right of=2] (3) {3};
\begin{scope}[->,thick]
\draw (1) -- (2);
\draw (3) -- (2);
\draw (2) to[out=-45,in=-45-90,looseness=5] (2);
\end{scope}
\draw [rounded corners=5mm,thick,dashed]
($(1) + (-6mm,5mm)$) rectangle ($(3) + (6mm,-20mm)$);
\node [right of=3,node distance=10mm,yshift=4.5mm] {{$\model{\amodel}$}};
\node [right of=2,node distance=12mm,yshift=-4.5mm] {$\model{\adomain}$};
\end{tikzpicture}}
\\[-4ex]
\hspace*{7ex}
\parbox{21ex}{\small
\hspace*{\fill}
$\model{\adomain} = \setexp{1,2,3}$\\[0.5ex]
\hspace*{\fill}
$\intin{\sunpred{R}}{\model{\amodel}}
= \setexp{ \pair{1}{2},\, \pair{2}{2},\, \pair{3}{2} } $}
}%
}
\pause{}
\vspace*{-2ex}
%
\begin{align*}
&
\model{\amodel} \satisfieslookup{\saluf} \formula{\existsst{y}{\forallst{x}{\,\binpred{R}{x}{y}}}} \;\;\uncover<10->{\alert{\checkmark}}
\\
& \uncover<3->{
\;\;\Longleftrightarrow\;\;
\text{there is $\forestgreen{b}\in\model{\adomain}$ such that: $\,$
$\model{\amodel} \satisfieslookup{\saluf[\freevar{y}\mapsto \forestgreen{b}]} \formula{\forallst{x}{\,\binpred{R}{x}{\freevar{y}}}}$}}
% \\[-0.75ex]
% & & & \uncover<3->{\hspace*{-2ex}\text{(by def.\ of $\ssatisfies$)}}
\\
& \uncover<4->{
\;\;\Longleftrightarrow\;\;
\parbox[t]{0.8\textwidth}
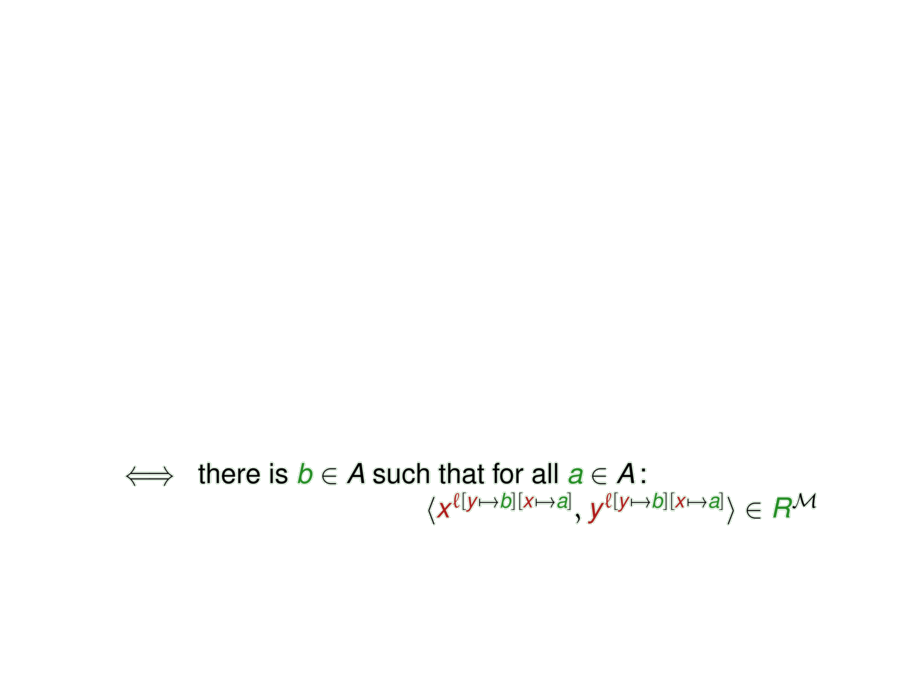
{there is $\forestgreen{b}\in\model{\adomain}$ such that for all $\forestgreen{a}\in\model{\adomain}\,$:\\
\hspace*{\fill}
$\model{\amodel} \satisfieslookup{\saluf[\freevar{y}\mapsto \forestgreen{b}][\freevar{x}\mapsto \forestgreen{a}]}
\formula{\binpred{R}{\freevar{x}}{\freevar{y}}}$}}
\\
& \uncover<5->{
\;\;\Longleftrightarrow\;\;
\parbox[t]{0.8\textwidth}
{there is $\forestgreen{b}\in\model{\adomain}$ such that for all $\forestgreen{a}\in\model{\adomain}\,$:\\
\hspace*{\fill}
\uncover<6->{$\pair{\forestgreen{a}}{\forestgreen{b}}
= }
\pair{\intin{\freevar{x}}{\saluf[\freevar{y}\mapsto \forestgreen{b}][\freevar{x}\mapsto \forestgreen{a}]}}
{\intin{\freevar{y}}{\saluf[\freevar{y}\mapsto \forestgreen{b}][\freevar{x}\mapsto \forestgreen{a}]}}
\in \intin{\sunpred{R}}{\model{\amodel}}$}}
\\
& \uncover<7->{
\;\;\Longleftarrow\;\;
\text{for all $\forestgreen{a}\in\model{\adomain}\,$ it holds that
$\pair{\forestgreen{a}}{2} \in \intin{\sunpred{R}}{\model{\amodel}}$}}
\\
& \uncover<8->{
\;\;\Longleftarrow\;\;
\pair{1}{2} \in \intin{\sunpred{R}}{\model{\amodel}}
\text{ and }
\pair{2}{2} \in \intin{\sunpred{R}}{\model{\amodel}}
\text{ and }
\pair{3}{2} \in \intin{\sunpred{R}}{\model{\amodel}}} \;\;\uncover<9->{\alert{\checkmark}}
\end{align*}\pause{}
\uncover<11->{%
This shows
$\model{\amodel} \satisfies \formula{\existsst{y}{\forallst{x}{\,\binpred{R}{x}{y}}}}$.}
%($\model{\amodel},\saluf$ satisfy $\formula{\existsst{y}{\forallst{x}{\,\binpred{R}{x}{y}}}}$).}
\end{exampleblock}
\end{frame}

