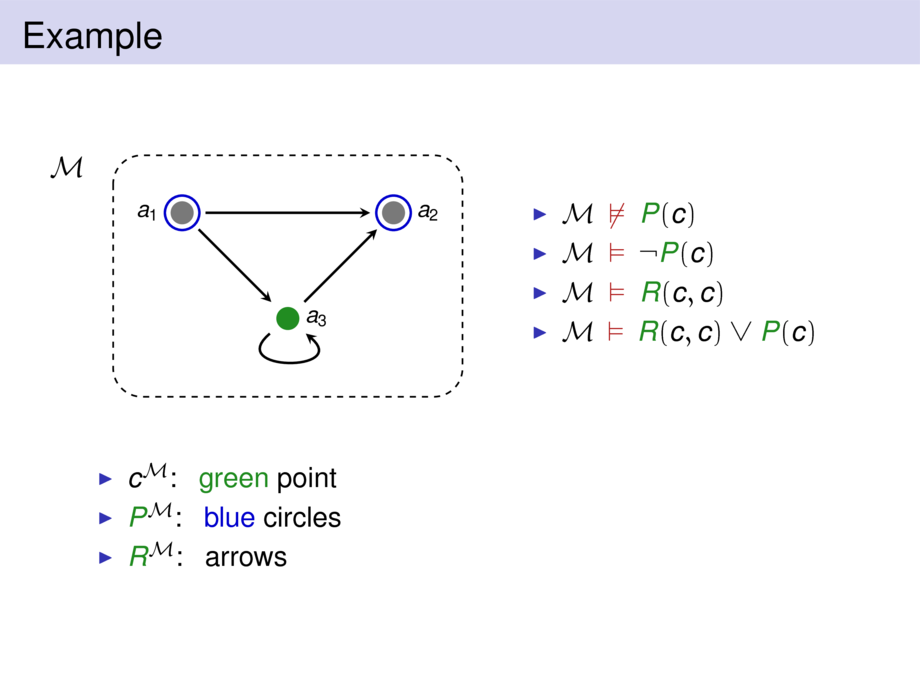


































































































94/270
\begin{frame}[t]{Interpreting Formulas Without Quantifiers}
\emph{Truth} definition for a formula $\formula{\aform}$
without quantifiers and free variables
in a model $\model{\amodel}$
by induction on the structure of $\formula{\aform}\,$:
%
\begin{itemize}\vspace*{1ex}\setlength{\itemsep}{1ex}
\pause
\item
$\model{\amodel} \satisfies \formula{\lognot{\aform}}
\begin{aligned}[t]
\mpause[1]{ & \;\iff\; \text{ not: } \model{\amodel} \satisfies \formula{\aform} }
\mpause{ \;\iff\; \model{\amodel} \satisfiesnot \formula{\aform} }
\end{aligned}$
\updatepause
\item
$\model{\amodel} \satisfies \formula{\logand{\aform}{\bform}}
\mpause[1]{ \;\iff\; \model{\amodel} \satisfies \formula{\aform}
\;\text{ and }\;
\model{\amodel} \satisfies \formula{\bform} }$
\updatepause
\item
$\model{\amodel} \satisfies \formula{\logor{\aform}{\bform}}
\mpause[1]{ \;\iff\; \model{\amodel} \satisfies \formula{\aform}
\;\text{ or }\;
\model{\amodel} \satisfies \formula{\bform} }$
\updatepause
\item
$\model{\amodel} \satisfies \formula{\logimp{\aform}{\bform}}
\begin{aligned}[t]
& \mpause[1]{ \;\iff\;
(\, (\model{\amodel} \satisfies \formula{\aform})
\implies (\model{\amodel} \satisfies \formula{\bform}) \,)} \\[-0.3ex]
& \mpause{ \;\iff\;
(\, \text{if }\;\; \model{\amodel} \satisfies \formula{\aform}
\;\;\text{ then }\;\; \model{\amodel} \satisfies \formula{\bform} \,)} \\[-0.3ex]
& \mpause{ \;\iff\;
\text{not } (\, \model{\amodel} \satisfies \formula{\aform}
\;\;\text{ and }\;\;
\model{\amodel} \satisfiesnot \formula{\bform} \,) }
\end{aligned}$
\updatepause
\item
$\model{\amodel} \satisfies \formula{\narypredsynvar{P}{\ateri{1},\ldots,\ateri{n}}}
\mpause{ \;\iff\; \tuple{ \interpretin{\formula{\ateri{1}}}{\model{\amodel}},
\ldots,
\interpretin{\formula{\ateri{n}}}{\model{\amodel}} }
\in \interpretin{\snarypredsynvar{P}}{\model{\amodel}} }$ \\[0.75ex]
\updatepause
\end{itemize}
\medskip
The last clause uses the \emph{interpretation of terms} $\intin{\formula{\ater}}{\model{\amodel}}$:
\begin{itemize}\setlength{\itemsep}{0.75ex}
\pause
\item
if $\formula{\ater} = \aconstsynvar$ for a constant $\aconstsynvar$,
then $\intin{\formula{\ater}}{\model{\amodel}} = \intin{\aconstsynvar}{\model{\amodel}}$
\pause
\item
if $\formula{\ater} = \formula{\afuncsynvar{\ateri{1},\ldots,\ateri{n}}}$,
then
$\intin{\formula{\ater}}{\model{\amodel}}
= \fap{\intin{\safuncsynvar}{\model{\amodel}}}
{\intin{\formula{\ateri{1}}}{\model{\amodel}},
\ldots,
\intin{\formula{\ateri{n}}}{\model{\amodel}}}$
\end{itemize}
\end{frame}

