\begin{frame}
  \frametitle{Examples: Semantics Intuitive}

  \begin{alertgoal}{}
    This is a typical exam task!
  \end{alertgoal}
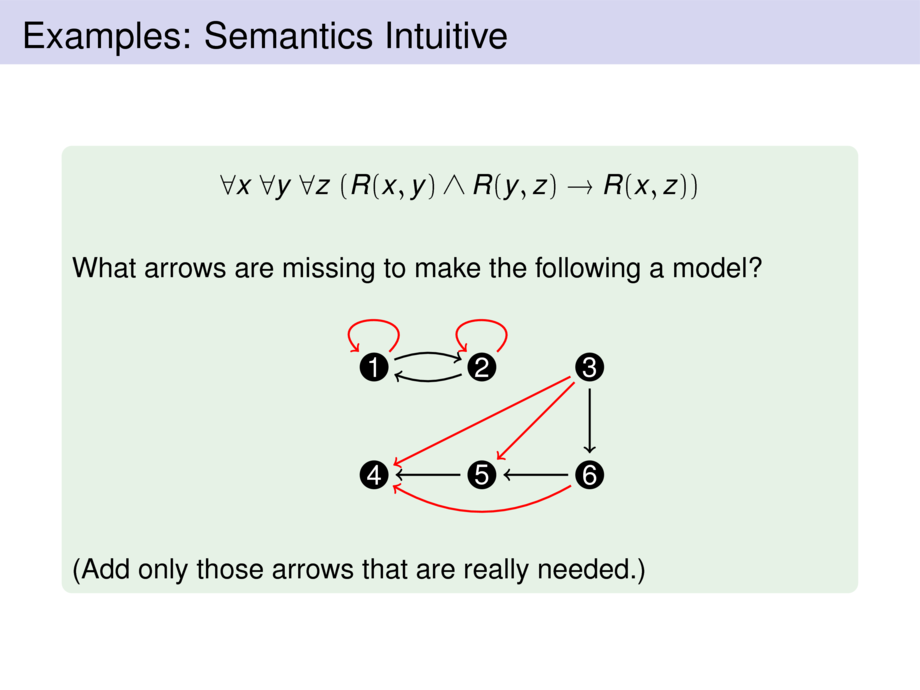
  \begin{exampleblock}{}
    \vspace{-1ex}
    \begin{talign}
      & \myall{x}{\myall{y}{\big(R(x,y) \vee R(y,x)\big)}}  \\
      & \wedge \myall{x}{\myall{y}{\myall{z}{\big(R(x,y) \wedge R(y,z) \to R(x,z)\big)}}} \\
      & \wedge \myall{x}{\myex{y}{\neg R(x,y)}}
    \end{talign}
    \pause

    Find a model for this formula, or explain why there is none. 
    \medskip
    \pause
    
    This formula has a model:
    \begin{itemize}
      \item universe $\nat = \{0,1,2,3,4,5\ldots\}$
      \item $R(x,y)$ if $x \ge y$
    \end{itemize}
    \pause
    We check that the formula holds in the model:
    \begin{itemize}
    \pause
      \item for all $x,y \in \nat$, we have $x \ge y \vee y \ge x$
    \pause
      \item for all $x,y,z \in \nat$, we have $x \ge y \wedge y \ge z \to x \ge z$
    \pause
      \item for every $x\in\nat$ there is $y\in\nat$ such that $x \not\ge y$
    \end{itemize}
  \end{exampleblock}
\end{frame}