



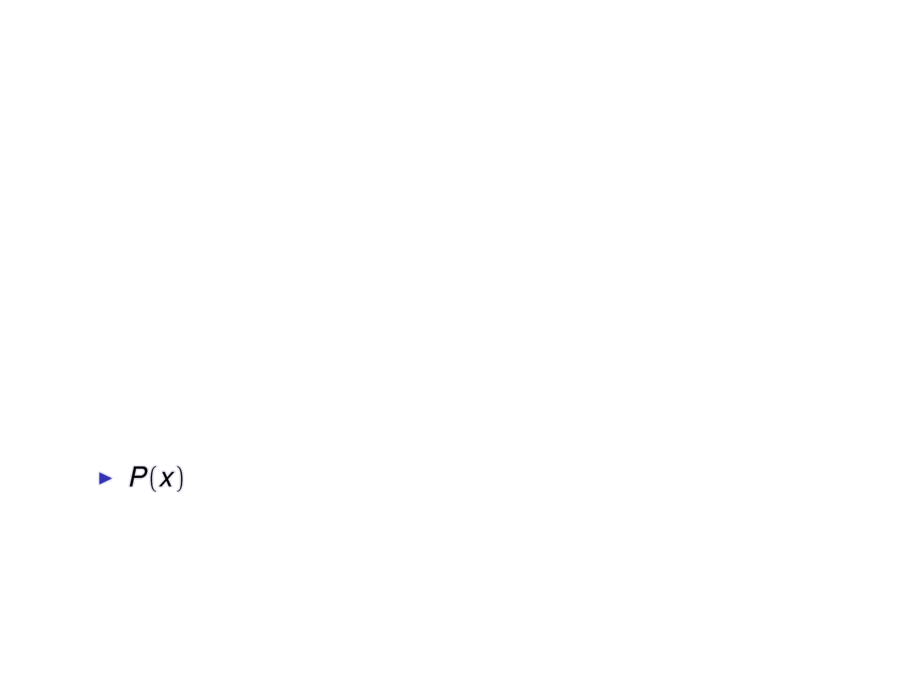































































































19/116
\begin{frame}
\frametitle{Formulas and Logic Connectives}
In predicate logic, the role of propositional variables is taken over by
the \aemph{atomic formulas}
with object/predicate-structure:
\begin{goal}{}
The \emph{atomic formulas} are predicates over objects:
\begin{itemize}
\item $P(x)$
\item $R(x,y)$
\end{itemize}
\end{goal}
\pause
\begin{goal}{}
Logic connectives $\;\neg,\; \vee,\; \wedge,\; \to\;$ keep their role.
\end{goal}
\pause
\begin{block}{}
We can build \emph{formulas} using propositional connectives,
starting from the smallest building blocks of atomic formulas:
\begin{itemize}
\pause
\item $P(x)$\quad\quad\pause\hint{($x$ is green)}
\pause
\item $P(x) \wedge R(x,y)$\quad\quad\pause\hint{($x$ is green and $x$ knows $y$)}
\pause
\item $R(x,y) \to \neg R(y,x)$\quad\quad\pause\hint{(if $x$ knows $y$ then $y$ does not know $x$)}
\end{itemize}
\end{block}
\pause
\begin{goal}{Predicate logic is more expressive}
In propositional logic, we could only state $p$, $p \wedge q$, $p \to \neg q$.
\end{goal}
\end{frame}

