\begin{frame}
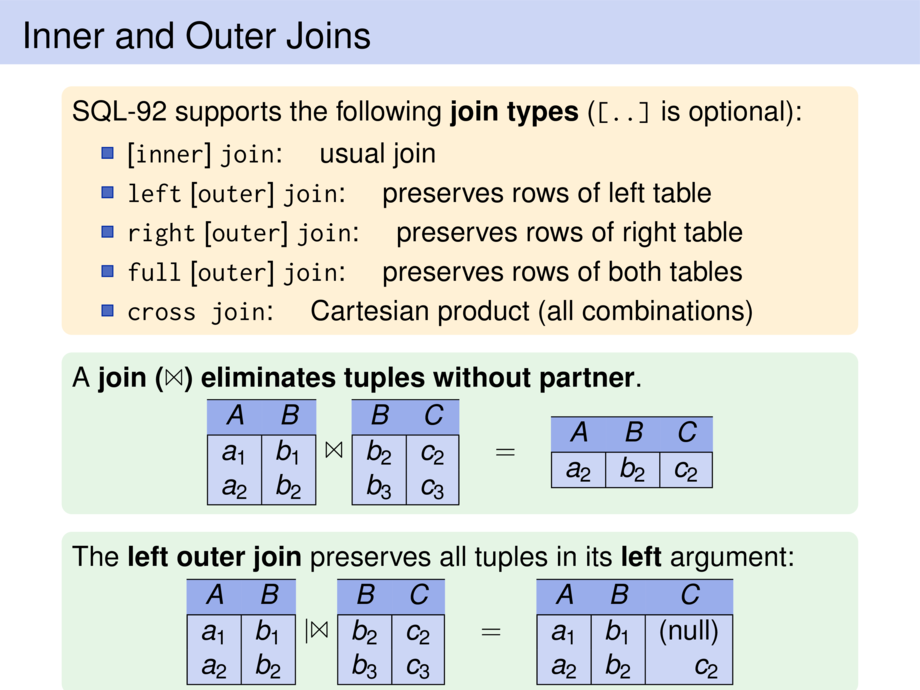
  \frametitle{Inner and Outer Joins}

  \vspace{-1ex}
  \begin{exampleblock}{}
    The \emph{right outer join} preserves all tuples in its \emph{right} argument:
    \begin{tcenter}
      $%
      \colorbox{rellight}{%
        $
        \begin{array}{|r|r|}
          \hline
          \hd{$A$} & \hd{$B$} \\ \hline
          a_1 & b_1 \\
          a_2 & b_2 \\
          \hline
        \end{array}$%
      }
      \Routerjoin
      \colorbox{rellight}{%
        $
        \begin{array}{|r|r|}
          \hline
          \hd{$B$} & \hd{$C$} \\ \hline
          b_2 & c_2 \\
          b_3 & c_3 \\
          \hline
        \end{array}$%
      }
      \quad=\quad
      \colorbox{rellight}{%
        $
        \begin{array}{|r|r|r|}
          \hline
          \hd{$A$} & \hd{$B$} & \hd{$C$} \\ \hline
          a_2 & b_2 & c_2 \\
          \text{(null)} & b_3 & c_3 \\
          \hline
        \end{array}$%
      }
      $
    \end{tcenter}
  \end{exampleblock}
  \pause
  \vspace{-.5ex}
  
  \begin{exampleblock}{}
    The \emph{full outer join} preserves all tuples in \emph{both} arguments:
    \begin{tcenter}
      $%
      \colorbox{rellight}{%
        $
        \begin{array}{|r|r|}
          \hline
          \hd{$A$} & \hd{$B$} \\ \hline
          a_1 & b_1 \\
          a_2 & b_2 \\
          \hline
        \end{array}$%
      }
      \Fouterjoin
      \colorbox{rellight}{%
        $
        \begin{array}{|r|r|}
          \hline
          \hd{$B$} & \hd{$C$} \\ \hline
          b_2 & c_2 \\
          b_3 & c_3 \\
          \hline
        \end{array}$%
      }
      \quad=\quad
      \colorbox{rellight}{%
        $
        \begin{array}{|r|r|r|}
          \hline
          \hd{$A$} & \hd{$B$} & \hd{$C$} \\ \hline
          a_1 & b_1 & \text{(null)} \\
          a_2 & b_2 & c_2 \\
          \text{(null)} & b_3 & c_3 \\
          \hline
        \end{array}$%
      }
      $
    \end{tcenter}
  \end{exampleblock}
  \pause
  \vspace{-.5ex}
  
  \begin{exampleblock}{}
    The \emph{cross join} is the \emph{Cartesian product}:
    \begin{tcenter}
      $%
      \colorbox{rellight}{%
        $
        \begin{array}{|r|r|}
          \hline
          \hd{$A$} & \hd{$B$} \\ \hline
          a_1 & b_1 \\
          a_2 & b_2 \\
          \hline
        \end{array}$%
      }
      \times
      \colorbox{rellight}{%
        $
        \begin{array}{|r|r|}
          \hline
          \hd{$B$} & \hd{$C$} \\ \hline
          b_2 & c_2 \\
          b_3 & c_3 \\
          \hline
        \end{array}$%
      }
      \quad=\quad
      \colorbox{rellight}{%
        $
        \begin{array}{|r|r|r|r|}
          \hline
          \hd{$A$} & \hd{$B$} & \hd{$B$} & \hd{$C$} \\ \hline
          a_1 & b_1 & b_2 & c_2 \\
          a_1 & b_1 & b_3 & c_3 \\
          a_2 & b_2 & b_2 & c_2 \\
          a_2 & b_2 & b_3 & c_3 \\
          \hline
        \end{array}$%
      }
      $
    \end{tcenter}
  \end{exampleblock}
\end{frame}